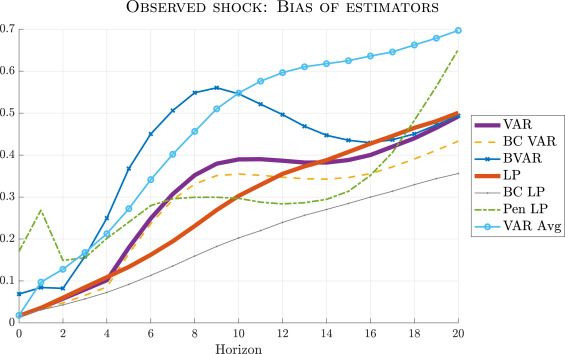
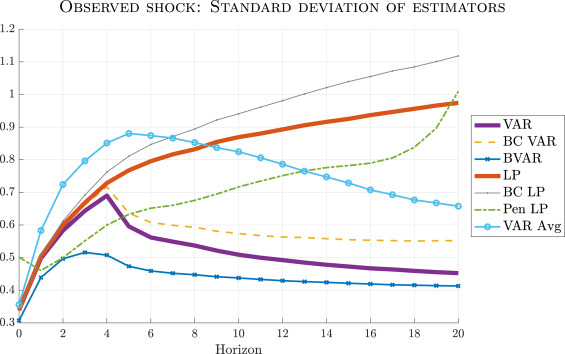
In a recent article published in the Journal of econometrics, we have some further insights about the bias-variance trade-off between IRF (Impulse Response Function) produced by the VAR and the LP methodologies with (very) extensive simulations for the universe of US macroeconomic data and with quarterly observations.
Li, D., Plagborg-Møller, M., & Wolf, C. K. (2024). Local projections vs. vars: Lessons from thousands of DGPs. Journal of Econometrics, 105722. https://doi.org/10.1016/j.jeconom.2024.105722
Some selected abstracts from their paper:
“Recently, Plagborg-Møller and Wolf (2021) proved that these two methods in fact estimate precisely the same impulse responses asymptotically, provided that the lag length used for estimation tends to infinity. This result holds regardless of identification scheme and regardless of the underlying data generating process (DGP).”
“How much more should one care about bias than variance to optimally choose the LP estimator over the VAR estimator in realistic sample sizes? And how does the trade-off depend on the DGP?“
“We find that the usual least-squares LP estimator tends to have lower bias than the least-squares VAR estimator, as expected, but also that this bias reduction comes at the cost of substantially higher variance. Out of all the procedures we analyze, bias-corrected LP is the most attractive estimator if and only if the researcher overwhelmingly prioritizes bias. If, however, the researcher also cares about precision (as in the conventional mean squared error criterion), then VAR methods are the most attractive.”
“Our findings provide a novel perspective on recent work emphasizing the potential dangers of VAR model misspecification (Ramey, 2016, Nakamura and Steinsson, 2018). We consider DGPs that do not admit finite-order VAR representations, so VAR methods indeed suffer from larger bias, as cautioned there. Reducing that bias via direct projection, however, tends to incur a steep cost in terms of increased sampling variance at intermediate and long horizons. Researchers who prefer to employ LP estimators should therefore be prepared to pay that price, and furthermore should apply the Herbst and Johannsen (2023) bias correction procedure when their data is persistent, as is usually the case.”
“Our findings point to several potential areas for future research. First, we conjecture that the bias–variance trade-off may differ quantitatively in panel data settings, to the extent that the availability of a large cross-section reduces the sampling variance of the estimators for a given time dimension, thus potentially making LP relatively more attractive than in the pure time series case. Second, our analysis has focused on the average performance of estimators across DGPs because we find that conventional model selection or evaluation tools are unable to detect substantial mis-specification of low-order VARs in our simulations; nevertheless, we view data-dependent estimator selection as an area ripe for further investigation.”
Before leaving, let me remind that you can estimate you can estimate Local Projections in EViews 14: