After my two first blogs on EViews programming, we are going to use Markov-Switching AR models to estimate current account persistence with quarterly data. AR stands for autoregressive. The code will produce the following Figures of the data and the smoothed regime probabilities:
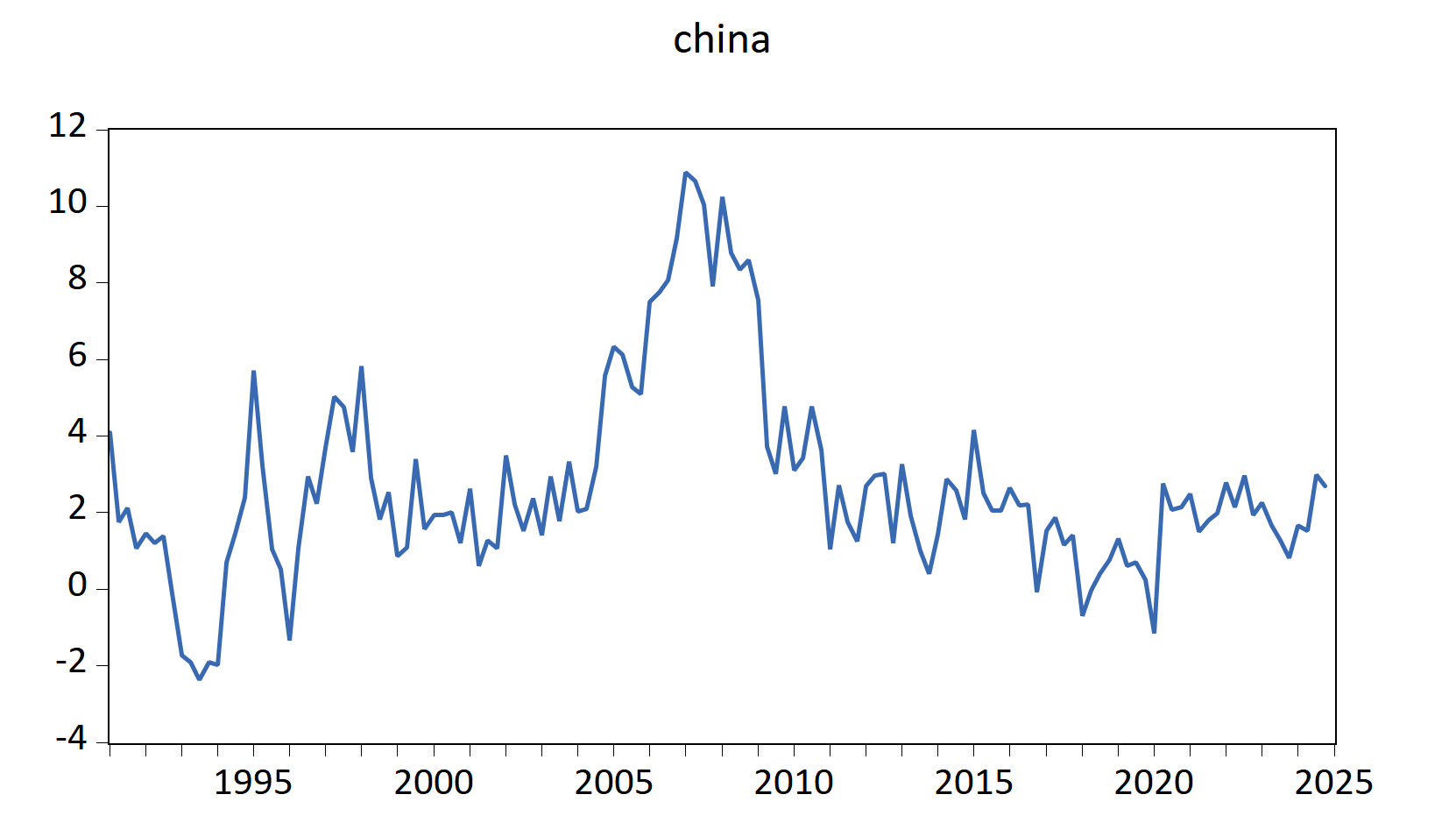
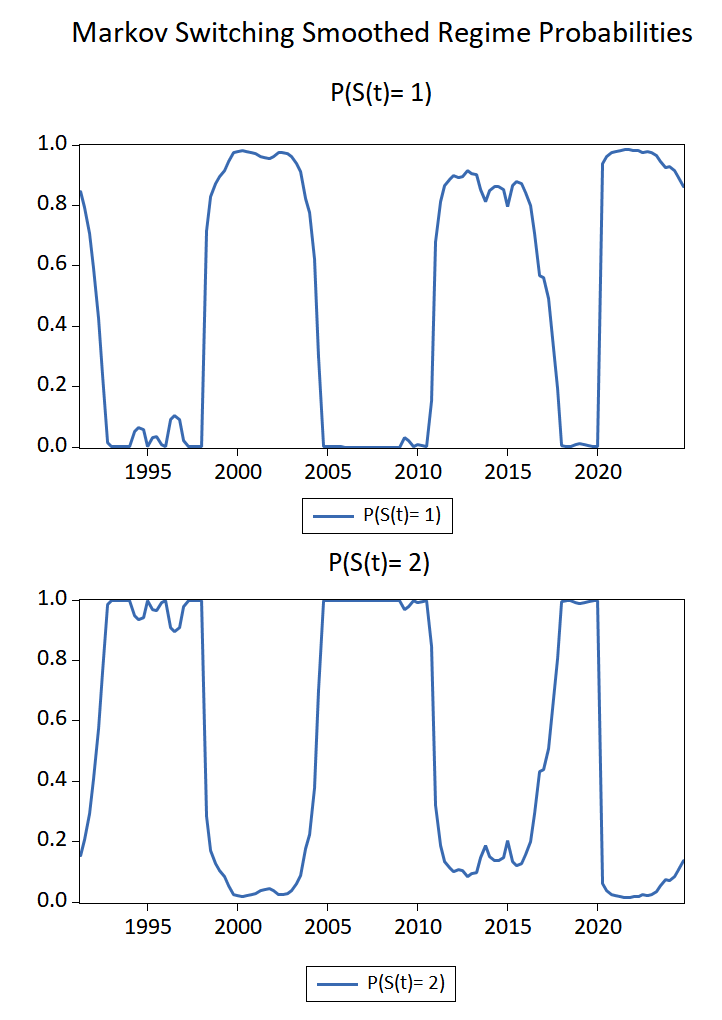
Now, we present the loop with a bit of programming. The data has to be organized in a wide format. I include China and Argentina for this small example and other countries can be included:
'Import data
import C:\Users\jamel\Dropbox\Latex\PROJECTS\22-11-cur-persistence\data\UPDATE_MAY_2025\reg_cab_data_wide.xlsx range=Sheet2 colhead=1 na="#N/A" @freq Q @id @date(series01) @smpl @all
'Program the loop
for %v ARGENTINA CHINA
smpl @all
smpl @ALL IF {%v}<>NA
show {%v}.line
equation eq{%v}
eq{%v}.switchreg(type=markov, nstates=2, heterr, covinfo=opg, seed=488352797) {%v} c ar(1)
eq{%v}.results
freeze(gr{%v}) eq{%v}.rgmprobs(type=smooth) 1 2
show gr{%v}
freeze(tb{%v}) eq{%v}.transprobs
show tb{%v}
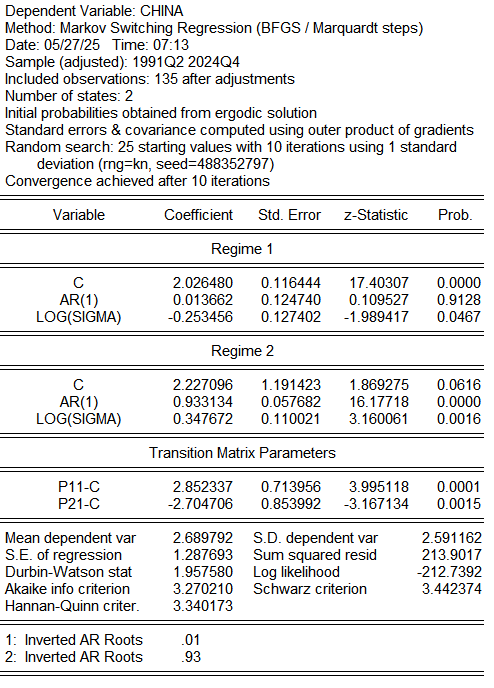
nextLet us examine the results for China, we have two regimes. The first one is a low-persistence regime and the second one is a high-persistence regime:
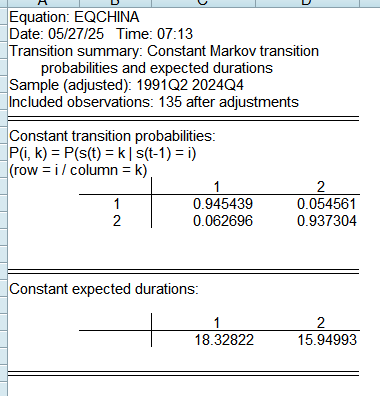
The transition matrix indicates the transition probabilities and the expected duration of each regime:
The smoothed regime probabilities indicates the temporal distribution of regimes. The Chinese current account was more persistent before the East Asian crisis, before 2010, and before the outbreak of the COVID-19:
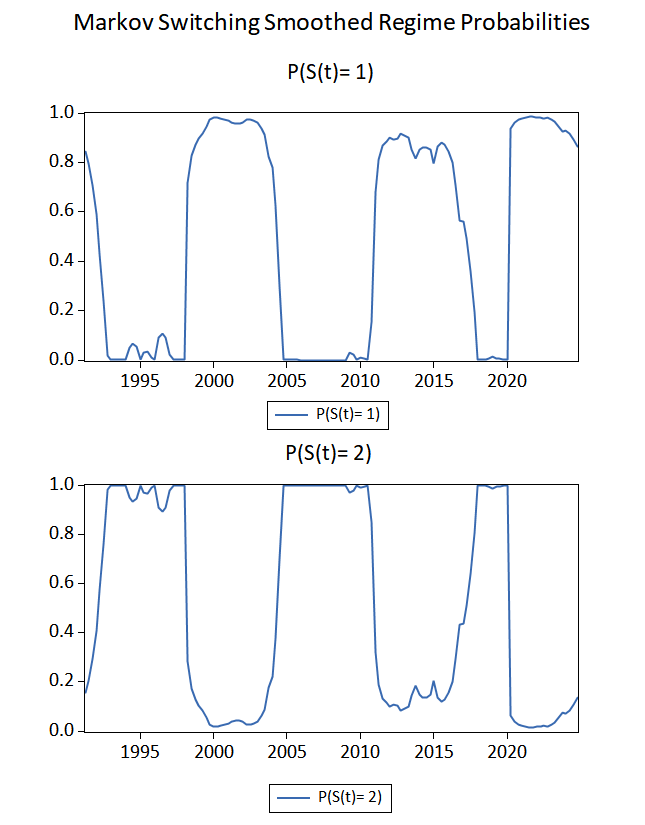
What about Argentina?
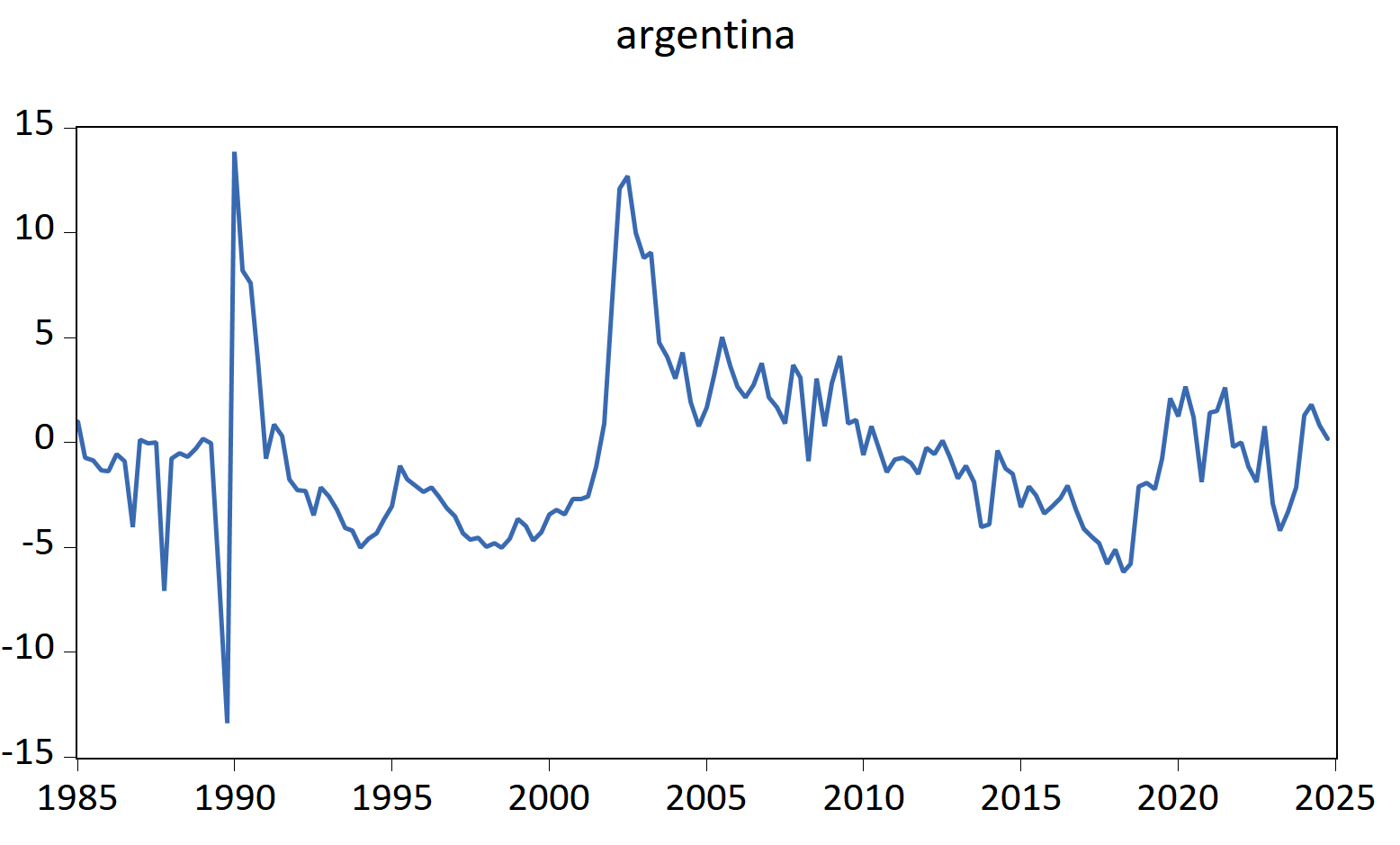
It appears that Argentina can be characterized by a 3-state Markov Switching AR model, you can slightly change the loop in the code in the following way:
for %v ARGENTINA
smpl @all
smpl @ALL IF {%v}<>NA
show {%v}.line
equation eq{%v}
eq{%v}.switchreg(type=markov, nstates=3, heterr, covinfo=opg, seed=488352797) {%v} c ar(1)
eq{%v}.results
freeze(gr{%v}) eq{%v}.rgmprobs(type=smooth) 1 2 3
show gr{%v}
freeze(tb{%v}) eq{%v}.transprobs
show tb{%v}
next
We have three regimes and the first one is very persistent, the second one is not very persistent, and the third one is mildly persistent:
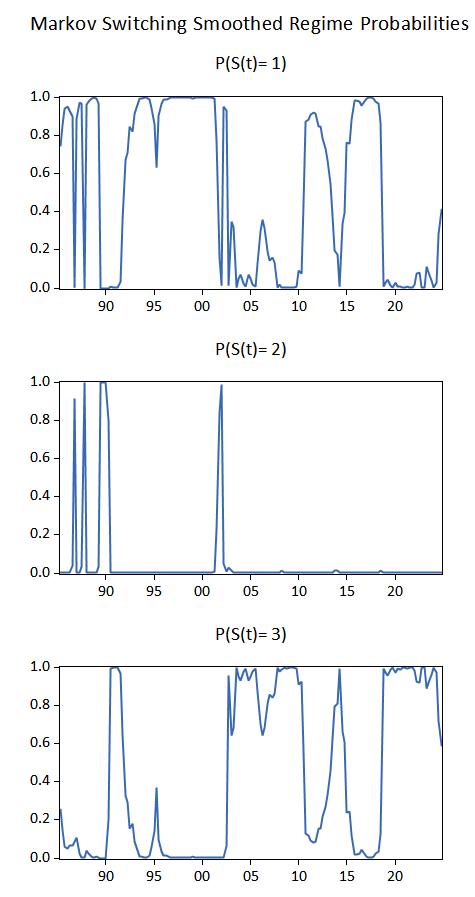
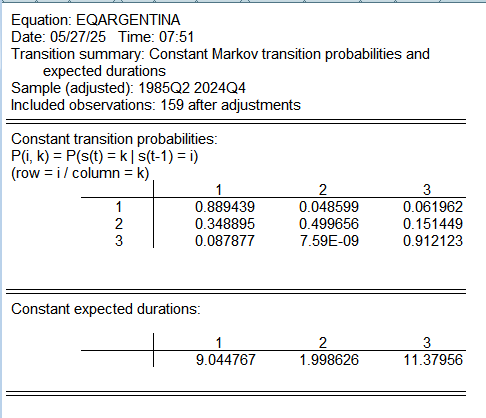
The transition probabilities indicate that the very persistent regime last less than 2 quarters and can be the synonym of crisis. The most recent period is characterized by less persistence (Regime 3) compared to the 90s and before the outbreak of the COVID-19:
Before leaving, allow me to share the following very handy EViews programming tutorial, that I found over the web: