Estima, the company that develops and sells the RATS software, has released a new version of their online help. Notably, they incorporated the user guide version of the chapter on VAR. The online chapter is a good balance between theory and application. We are going to use the data covered in this publication, that relates oil price dynamics to the political tensions between the US and China in order to illustrate the commands to get the impulse response functions (IRF), historical decompositions (HD), and variance decompositions (VD). Let me remind that I already covered similar commands in the following two blogs: “Local Projection with Stata” and “Moving Block Bootstrap with GAUSS” using a similar dataset. The full code is available on my GitHub. Special thanks go to Francisco Serranito for his RATS lectures during my Master’s thesis.
I start with the impulse response functions using Monte Carlo Integration for the confidence bands, please refer to this part of the help for more details. I will import the data and make the necessary transformation for the variables.
OPEN DATA "C:\Users\jamel\Dropbox\Latex\PROJECTS\23-05-geopolitical-risk-pol-tension-oil-price\Data and command\lpirf_PRI_GPR.dta"
CALENDAR(M) 1960:1
DATA(FORMAT=DTA,RIGHT=9) 1960:01 2019:12 PERIOD PRI PRI_S PRO RPO DEM DINV GPRCN IGREA
set lpri = PRI_S
set lpro = 1*log(PRO)
set lrpo = 1*log(RPO)
set ldem = 1*log(DEM)Now, I have to specify the VAR system with the appropriate number of lags and steps for the visualization of the IRF. With the @montevar procedure, I will compute the confidence bands for the VAR. In the help, they mention that “The shocks are in the columns and the response variables are in the rows.”
*****************************************************************
compute nlags = 24
compute nsteps = 48
system(model=prirpo)
variables lpri ldem lpro lrpo
lags 1 to nlags
det constant
end(system)
compute implabel=|| $
"Political Relations",$
"Oil Demand",$
"Oil Production",$
"Real Price"||
estimate(noprint) 1989:01 2019:12
@montevar(draws=4000,model=prirpo,$
shocks=implabel,varlabels=implabel$
header="IRF's with Error Bands")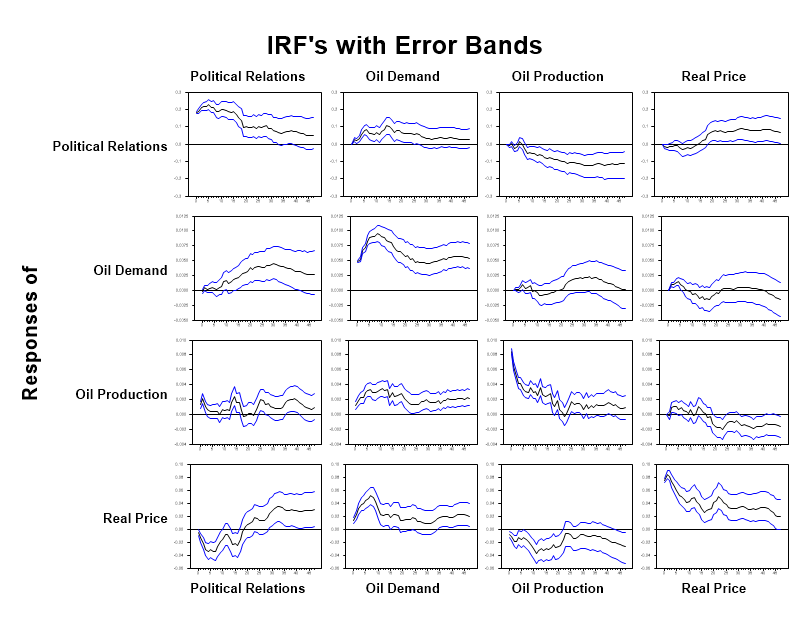
In the first column, we can observe the effect of an identified shock of political relations between the US and China on the oil market, for more detail, please consult this article.
We can turn now to the HD. First, I have to include the forecast horizon. In this example, I will choose a forecasting period from January 2003 to December 2019. Then, I declare the variable labels and include some code that will be helpful in the loop to produce the graphs. The HD are computed using the @history function. The loop allows computing HD for each variable. Let us focus on the real price of oil in log. They mention that “With this color scheme, the black line is the actual data, the blue is the base forecast (which starts a year into the graph) and the green is the base forecast plus the effects of the shock”.
compute hstart = 2003:1
compute hend = 2019:12
compute varlabels=|| $
"Real Price",$
"Oil Production",$
"Oil Demand",$
"Political Relations"||
compute neqn=%modelsize(prirpo)
dec vect[int] depvar(neqn)
dec vect[string] varlabels(neqn) shocklabels(neqn)
ewise varlabels(i)=%modellabel(prirpo,i)
ewise shocklabels(i)=%modellabel(prirpo,i)
compute depvar=%modeldepvars(prirpo)
estimate(noprint,noftests,resids=resids) 1989:01 2019:12
HISTORY(MODEL=PRIRPO,add,base=base,effects=effects,FROM=2003:01,TO=2019:12,PRINT)
compute rows=fix(sqrt(neqn))
compute cols=(neqn-1)/rows+1
do i=1,neqn
spgraph(vfields=rows,hfields=cols,window=varlabels(i),$
header="Historical Decomposition of "+varlabels(i))
do j=1,neqn
*
* This graphs the actual data (including four pre-sample values),
* the base forecast, and the effects of shock J on variable I.
*
graph(header="Effect of "+shocklabels(j)) 3
# depvar(i) hstart-4 hend
# base(i)
# effects(i,j)
end do j
spgraph(done)
end do i
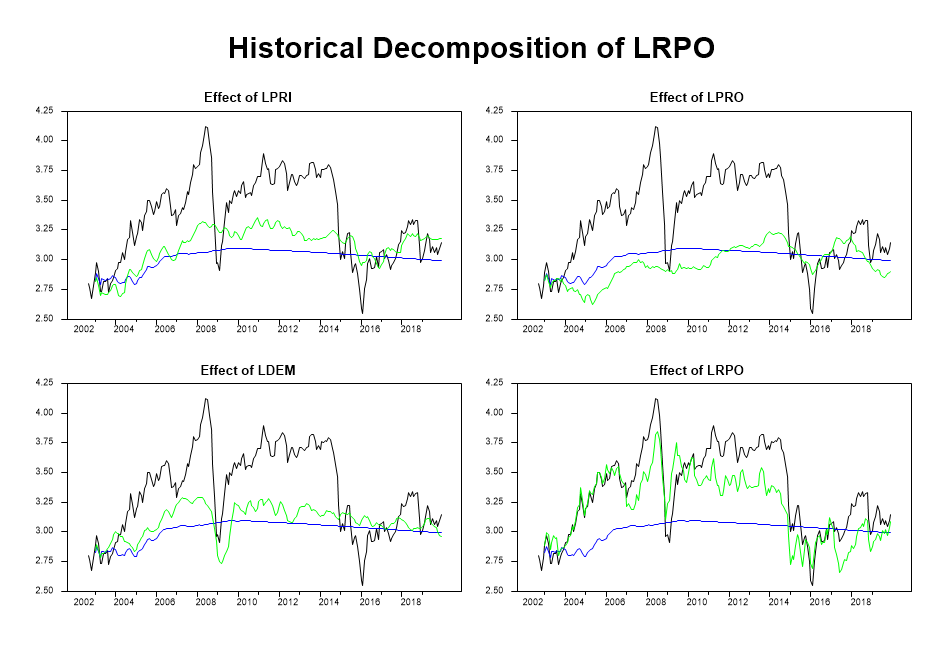
We can observe that the political relations between the US and China contributed positively to oil prices during the GFC and the fall of commodity prices in 2016.
Let us conclude this blog with the VD. I will use the ERROR instruction over 48 months to capture the long-lasting effect of political relations on the oil price.
*****************************************************************
system(model=prirpo)
variables lpri ldem lpro lrpo
lags 1 to 24
det constant
end(system)
estimate(cvout=v,noprint) 1989:01 2019:12
*
* The first decomposition is done in the original order:
* system(model=prirpo)
* lpri ldem lpro lrpo.
*
ERRORS(MODEL=PRIRPO,STEPS=48,PRINT)
*****************************************************************We can observe that innovations on political relations explain 17.38% of the variance of the one-step forecast error for the oil prices at the horizon of 48 months.
Decomposition of Variance for Series LRPO
Step Std Error LPRI LDEM LPRO LRPO
1 0.06569657 0.549 2.935 1.293 95.223
2 0.10028101 1.410 4.898 1.468 92.224
3 0.12768230 3.057 7.413 2.425 87.105
4 0.14945727 5.311 10.216 3.003 81.470
5 0.16610357 7.384 12.500 2.860 77.256
6 0.18036029 8.421 14.910 2.987 73.682
7 0.19271057 9.595 17.552 2.959 69.895
8 0.20462953 10.483 20.109 3.092 66.316
9 0.21439487 10.675 22.103 3.431 63.791
10 0.22218547 10.490 23.357 4.187 61.965
11 0.22842352 10.285 23.388 5.202 61.124
12 0.23499869 9.801 22.763 6.757 60.679
13 0.24118163 9.376 22.172 7.783 60.669
14 0.24642067 9.303 21.808 8.508 60.381
15 0.25172207 9.580 21.452 9.395 59.574
16 0.25559427 9.859 21.144 10.115 58.882
17 0.25950074 10.231 21.041 10.873 57.855
18 0.26274478 10.216 21.055 11.452 57.277
19 0.26530778 10.032 21.104 11.795 57.069
20 0.26802469 9.849 20.868 12.350 56.933
21 0.27151787 9.664 20.516 12.757 57.063
22 0.27525937 9.485 20.151 12.962 57.402
23 0.27941861 9.342 19.766 12.828 58.063
24 0.28297700 9.420 19.490 12.545 58.545
25 0.28583711 9.462 19.366 12.330 58.842
26 0.28833113 9.472 19.265 12.164 59.100
27 0.29036112 9.506 19.125 12.152 59.217
28 0.29222649 9.560 18.991 12.152 59.296
29 0.29414391 9.703 18.835 12.089 59.373
30 0.29631012 10.069 18.629 11.969 59.333
31 0.29877318 10.554 18.389 11.829 59.228
32 0.30160973 11.176 18.106 11.672 59.047
33 0.30467669 11.887 17.822 11.521 58.770
34 0.30770065 12.573 17.623 11.379 58.425
35 0.31047493 13.180 17.511 11.235 58.074
36 0.31306040 13.638 17.476 11.126 57.760
37 0.31569872 14.032 17.452 11.033 57.483
38 0.31830341 14.435 17.448 10.933 57.184
39 0.32107546 14.827 17.419 10.876 56.878
40 0.32378098 15.148 17.363 10.855 56.634
41 0.32645988 15.453 17.293 10.864 56.390
42 0.32927545 15.712 17.279 10.916 56.092
43 0.33206894 15.943 17.312 10.989 55.756
44 0.33481253 16.232 17.355 11.083 55.330
45 0.33743505 16.516 17.416 11.229 54.839
46 0.33997976 16.801 17.491 11.433 54.276
47 0.34247046 17.087 17.545 11.671 53.697
48 0.34504562 17.385 17.551 11.940 53.124