Do we really read papers in economics?

Last Friday, I had the chance to welcome Joshua Aizenman for a research seminar at the University of Strasbourg: https://www.beta-economics.fr/.

We had an interesting discussion about this provocative question: Do we really read papers in economics?

This question may appear provocative. But, let me add two elements that could push you into some unexpected directions.

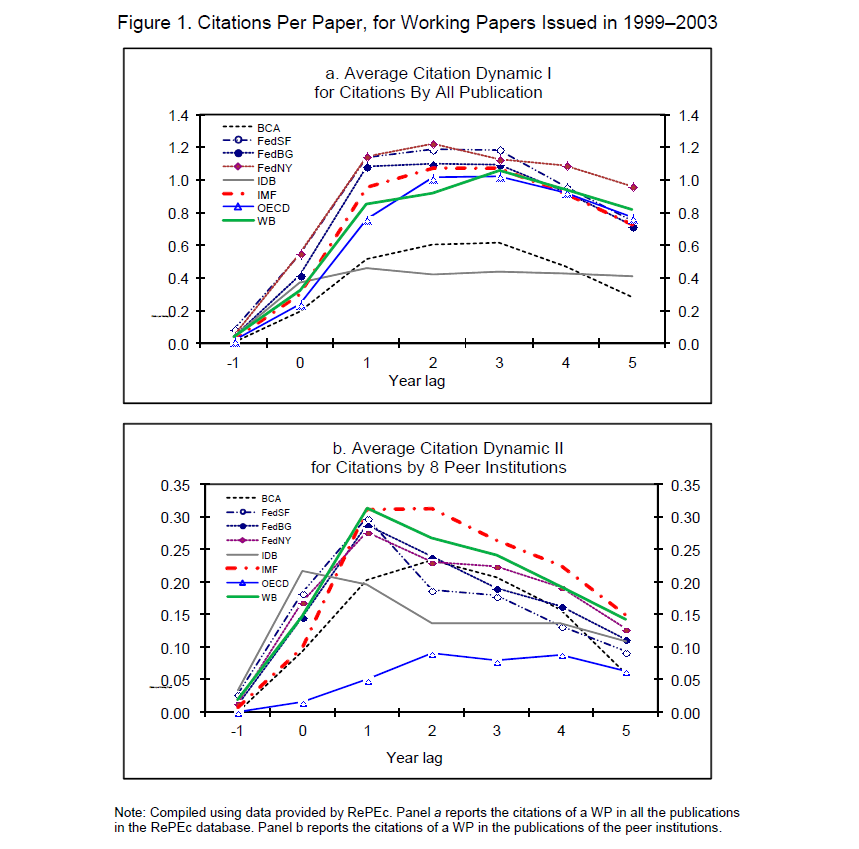
First, the number of papers’ citation seems to peak after two years in well established institutions, according to the following study: Evaluating_the_Quality_of_IMF_Research.

A duration to peak in citations of two years on average may explain why economics could be memoryless about past contributions.

Second, let us look at a case study. According to Wikipedia, the endogenous growth theory was introduced in the mid-1980s:

But, wait, is it really the case? In an unnoticed AER article (https://www.jstor.org/stable/1812179), Marvin Frankel wrote in 1962 a contribution that includes “many of the features of the models found in Paul M. Romer (1986), Robert E. Lucas, Jr. (1988), and Sergio Rebelo (1991).” according to Edmund S. Cannon in AER article in 2000 (https://www.jstor.org/stable/117294).

I continue to quote Cannon’s paper:

“Substituting this back into the firm’s production function and summing over i, one obtains the aggregate production function

\begin{aligned}
Y&=A K^\theta L^\phi , \\
\theta &\equiv \beta+\gamma, \\
\phi &\equiv 1-\beta+\gamma^{\prime} .
\end{aligned}

Because firms face diminishing marginal returns, there will be a competitive equilibrium, but at the aggregate level the returns to capital will be greater and there may be economies of scale.

The structure of this model is similar to Romer (1986), where γ’ = 0 and the capital is knowledge: Romer’s footnote 6 observes that knowledge may need to be embodied in other forms of capital.

Frankel considers several possibilities:

1. A standard neoclassical model: θ+φ = 1. Although the conclusion of the neoclassical growth model that saving does not affect the growth rate is still valid, standard growth accounting is invalid because factor shares do not measure marginal products;
2. An “AK” model where output is linear in capital: θ = 1, φ = 0. In this model, the savings rate directly determines the growth rate;
3. An increasing returns-to-scale model: θ + φ > 1.

The only possibility that Frankel does not consider explicitly is that θ > 1.”

Now, I stop to quote Cannon’s paper.

Probably, quoting old papers is not a bad thing, after all. As in life, timing and luck are essential factors in economics.

In this respect, Aizenman and Kletzer (2008) explain the importance of “being there”: https://cepr.org/

“Researchers play a role in promoting their own research simply by being visible to the research community and continuing to press a current research agenda through presentations and follow-up papers.”