Today, we will see how to translate the first part of the code the threshold VAR model in Balke (2000) using ChatGPT5. It took me a few hours and some iterations. The paper is available here. As explained on the Estima website, the first part of the code, tvar_estimate.rpf, tests for a threshold break and estimates the model.
Key takeaways:
- ChatGPT 5 is quite powerful to translate RATS codes to Stata codes;
- It still makes silly mistakes like calling nonexistent variables or opening and closing loop brackets on the same line;
- The threshold value is the same in the RATS code for the credit variable;
- The LR Statistics are higher in my Stata code;
- The RATS bootstrap is much faster than the one I coded.
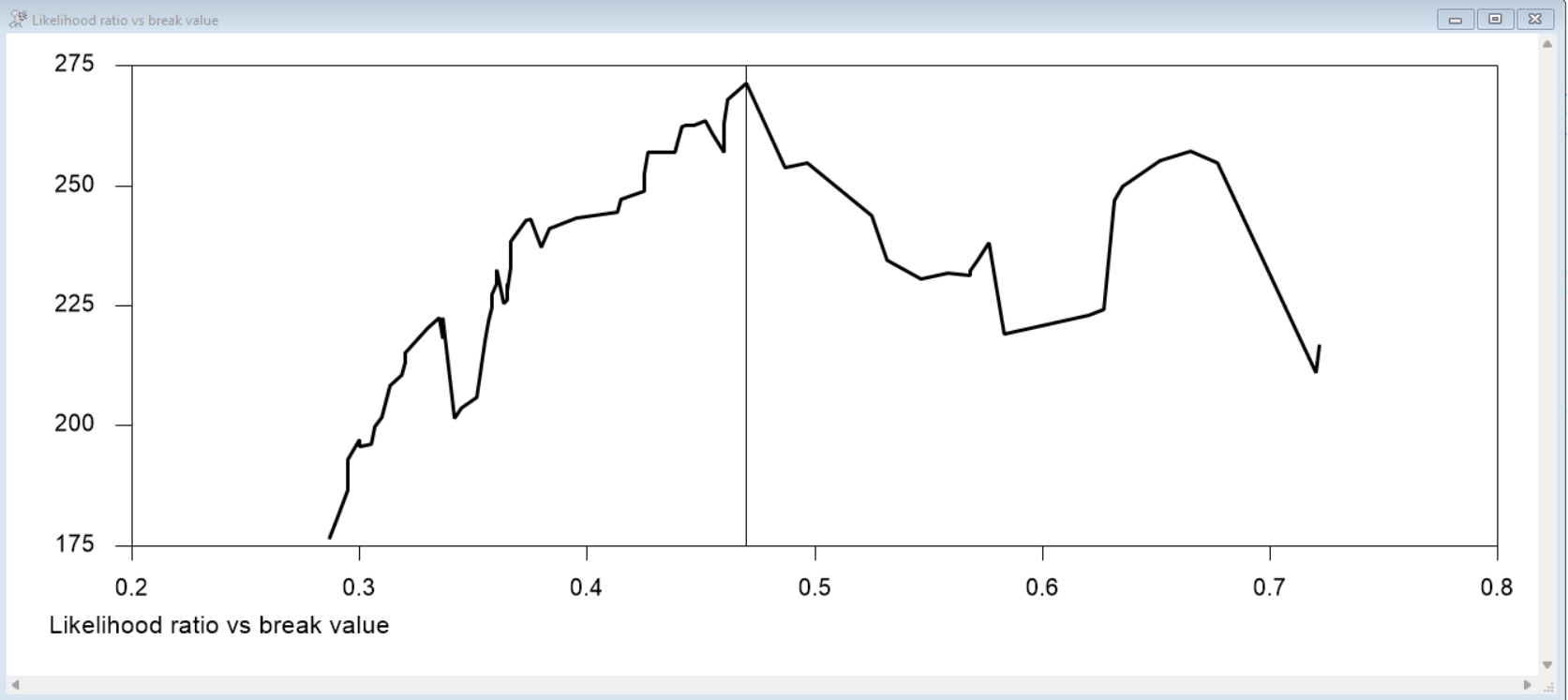
I managed to replicate the Likelihood Ratio versus break figure. The following Figure is from the RATS code.
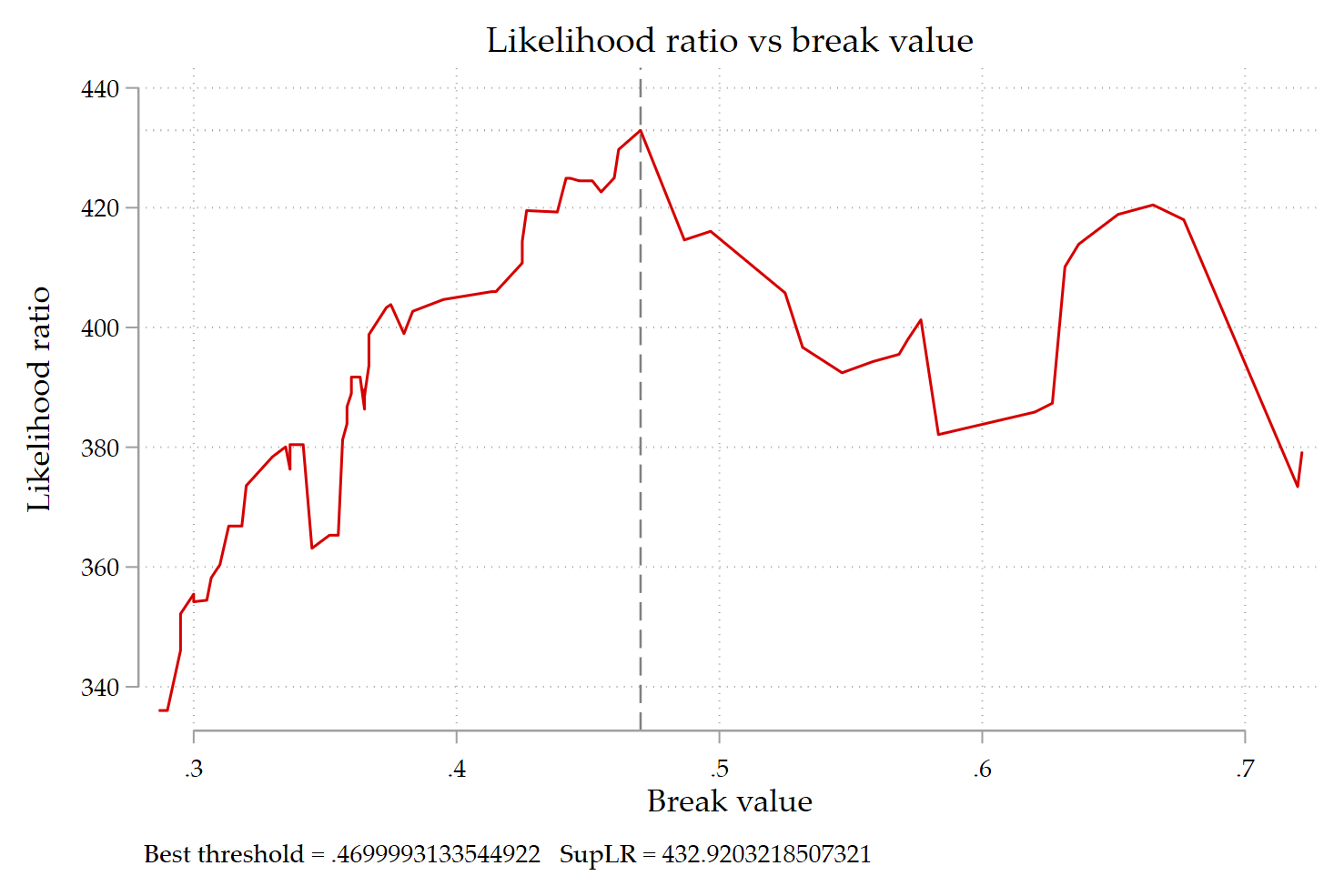
The figure below is from the Stata code that I wrote, the pattern is almost identical:


The full code is explained below, and the update will be available on my GitHub :
capture log close _all
log using TVAR_Part1_Aug25.log, name(TVAR_Part1_Aug25) text replace
/******************************************************************
Threshold VAR (Balke 2000) — FULL Stata code (globals only)
- No tsset / time index required
- Manual lags/MA/delay with row subscripts
- Pure Stata matrices (no frames, no postfile, no Mata)
- Never drops S
- Produces tempfiles: data_dta, LRGRID_dta, GAMMA_LIST
******************************************************************/
clear
clear matrix
cls
cd C:\Users\jamel\Dropbox\Documents\blog-data\2025-blog\Threshold_VAR
import excel "dataset.xlsx", sheet("Sheet1") firstrow clear
/***********************
0) PARAMETERS (GLOBALS)
***********************/
global PI 0.15 // grid trimming at each end
global MAXLAG 4 // max VAR lag
global D 1 // delay for threshold q = credthr[_n - D]
global MALENGTH 2 // lagging MA span for threshold series
global NBOOT 100 // bootstrap replications
/*************************
1) VARIABLES (GLOBALS)
*************************/
global YLIST d1y d1p money credit
global NVARS : word count $YLIST
/*********************
2) TRANSFORMATIONS
*********************/
capture drop mix d1mix gdp pgdp cpbill1 d1gdp d1pgdp ly d1y d1p money credit
gen double mix = (nfbstk + nfcstk)/(cmpapstk + nfbstk + nfcstk)
gen double gdp = rgdpcw
gen double pgdp = pgdpcw
gen double d1mix = mix - mix[_n-1]
gen double cpbill1 = cp46 - t6
gen double d1gdp = 400*ln(gdp/gdp[_n-1])
gen double d1pgdp = 400*ln(pgdp/pgdp[_n-1])
gen double ly = ln(gdp)
gen double d1y = d1gdp
gen double d1p = d1pgdp
gen double money = fyff
gen double credit = cpbill1
capture drop tindex
gen long tindex = _n // simple row index
/*****************************************
3) UTILITIES (NO tsset / Mata / frames)
*****************************************/
capture program drop __make_lags
program define __make_lags
syntax varlist, P(integer)
foreach v of varlist `varlist' {
forvalues k = 1/`p' {
capture drop L`k'_`v'
gen double L`k'_`v' = `v'[_n-`k'] if _n>`k'
}
}
end
capture program drop __build_laglist
program define __build_laglist
syntax, P(integer)
global LAGLIST
forvalues k = 1/`p' {
foreach v of global YLIST {
global LAGLIST $LAGLIST L`k'_`v'
}
}
end
capture program drop __mark_sample
program define __mark_sample
syntax, P(integer)
capture drop ok_dep ok_lags S_lin
gen byte ok_dep = 1
foreach v of global YLIST {
replace ok_dep = 0 if missing(`v')
}
gen byte ok_lags = 1
foreach x of global LAGLIST {
replace ok_lags = 0 if missing(`x')
}
gen byte S_lin = ok_dep & ok_lags
end
/********************************************
4) FIND FEASIBLE LAG ORDER (<= $MAXLAG)
********************************************/
global PFEAS .
forvalues pcur = $MAXLAG(-1)1 {
__make_lags $YLIST, p(`pcur')
__build_laglist, p(`pcur')
__mark_sample, p(`pcur')
quietly count if S_lin
if (r(N)>0) {
global P `pcur'
global LAGLIST_KEEP "$LAGLIST"
global PFEAS 1
continue, break
}
}
if "$PFEAS"=="." {
di as err "No rows with complete lags even at p=1. Check missing values or row order."
exit 2000
}
global LAGLIST $LAGLIST_KEEP
di as txt "Using lag order p = " as res $P
* align with chosen p
__make_lags $YLIST, p($P)
__build_laglist, p($P)
__mark_sample, p($P)
/********************************************
5) BASELINE LINEAR VAR (eq-by-eq OLS)
********************************************/
scalar SIG0DET = .
scalar TOBS = .
scalar RSS0 = 0
foreach y of global YLIST {
quietly regress `y' $LAGLIST if S_lin
predict double `y'_e0 if e(sample), resid
scalar RSS0 = RSS0 + e(rss)
if missing(TOBS) scalar TOBS = e(N)
}
* ln|Sigma0| from residuals (pure Stata matrices)
local rlist
foreach y of global YLIST {
local rlist `rlist' `y'_e0
}
mkmat `rlist' if S_lin, matrix(U0)
scalar T0 = rowsof(U0)
matrix S0 = (U0'*U0)/T0
matrix symeigen L0 V0 = S0
local k = colsof(S0)
scalar SIG0DET = 0
forvalues i=1/`k' {
scalar SIG0DET = SIG0DET + ln(L0[`i',`i'])
}
/******************************************************
6) THRESHOLD VARIABLE (manual MA + delay; no tsset)
******************************************************/
capture confirm variable S_lin
if _rc {
__make_lags $YLIST, p($P)
__build_laglist, p($P)
__mark_sample, p($P)
}
capture drop credthr
gen double credthr = 0
forvalues i = 1/$MALENGTH {
replace credthr = credthr + cond(missing(credit[_n-(`i'-1)]), 0, credit[_n-(`i'-1)])
}
replace credthr = credthr / $MALENGTH
capture drop q
gen double q = credthr[_n - $D] if _n > $D
gen byte S = S_lin & !missing(q)
* Never drop S
capture confirm variable S
if _rc gen byte S = S_lin & !missing(q)
else replace S = S_lin & !missing(q)
capture drop S_idx
gen long S_idx = .
replace S_idx = sum(S) if S==1
/*********************************************
SAVE ORIGINAL DATA FOR STEP 9 & BOOTSTRAP
*********************************************/
tempfile data_dta
save "`data_dta'", replace
/***************************************************************
7) BUILD THRESHOLD GRID (unique q, trimmed by PI and nreg)
***************************************************************/
preserve
keep if S==1
keep q
sort q
by q: keep if _n==1
gen long rank = _n
count
local Nobs = r(N)
global NREG = $NVARS * $P + 1
local piskip = floor($PI*`Nobs') + $NREG
local pistart = 1 + `piskip'
local piend = `Nobs' - `piskip'
if (`piend' < `pistart') {
restore
di as err "Trimming leaves no candidates. Reduce PI or P."
exit 498
}
keep if inrange(rank, `pistart', `piend')
levelsof q, local(GAMMAS)
restore
/*************************************************************
Helper: residual covariances at a given gamma (Stata only)
*************************************************************/
capture program drop _tvar_lls
program define _tvar_lls, rclass
syntax , GAMMA(real)
tempvar R1 R2 C1 C2
gen byte `R1' = (q <= `gamma') if S==1
gen byte `R2' = (q > `gamma') if S==1
gen double `C1' = `R1'
gen double `C2' = `R2'
* regime-specific design
global X1 `C1'
global X2 `C2'
forvalues k = 1/$P {
foreach v of global YLIST {
tempvar z1 z2
gen double `z1' = L`k'_`v' * `R1'
gen double `z2' = L`k'_`v' * `R2'
global X1 $X1 `z1'
global X2 $X2 `z2'
}
}
tempname OK
scalar `OK' = 1
foreach y of global YLIST {
quietly regress `y' $X1 $X2 if S==1, noconstant
scalar `OK' = `OK' * (e(N)>0)
capture drop `y'_e
predict double `y'_e if e(sample), resid
}
quietly count if S==1 & `R1'==1
scalar T1cnt = r(N)
quietly count if S==1 & `R2'==1
scalar T2cnt = r(N)
scalar `OK' = `OK' * (T1cnt>0) * (T2cnt>0)
return scalar ok = `OK'
if (`OK'==0) exit
local rlist
foreach y of global YLIST {
local rlist `rlist' `y'_e
}
mkmat `rlist' if S==1, matrix(Uh)
scalar Th = rowsof(Uh)
matrix Sh = (Uh'*Uh)/Th
scalar lnDetSh = ln(det(Sh))
mkmat `rlist' if S==1 & `R1'==1, matrix(U1)
scalar T1 = rowsof(U1)
matrix S1 = (U1'*U1)/T1
scalar lnDetS1 = ln(det(S1))
mkmat `rlist' if S==1 & `R2'==1, matrix(U2)
scalar T2 = rowsof(U2)
matrix S2 = (U2'*U2)/T2
scalar lnDetS2 = ln(det(S2))
return scalar ok = 1
return scalar lnDetSh = lnDetSh
return scalar lnDetS1 = lnDetS1
return scalar lnDetS2 = lnDetS2
return scalar T = Th
return scalar T1 = T1
return scalar T2 = T2
end
/*********************************************************
8) SCAN GAMMA GRID — brace-free indexed loop
**********************************************************/
matrix drop _all
local bestLR = .
local bestg = .
local NG : word count `GAMMAS'
forvalues i = 1/`NG' {
local g : word `i' of `GAMMAS'
quietly _tvar_lls, gamma(`g')
if !r(ok) continue
scalar LLhet = -0.5*( r(T1)*r(lnDetS1) + r(T2)*r(lnDetS2) )
scalar LLhom = -0.5*( r(T) * r(lnDetSh) )
scalar LLlin = -0.5*( r(T) * SIG0DET )
scalar LRh_ = 2*(LLhet - LLlin)
scalar LRm_ = 2*(LLhom - LLlin)
matrix row = (`g', LRh_, LRm_)
capture matrix LRGRID = LRGRID \ row
if _rc matrix LRGRID = row
if missing(`bestLR') | (LRh_ > `bestLR') local bestLR = LRh_
if missing(`bestg') | (LRh_ >= `bestLR') local bestg = `g'
}
capture confirm matrix LRGRID
if _rc {
di as err "LRGRID is empty: no valid gamma produced r(ok)=1. Check data/grid."
exit 2001
}
matrix colnames LRGRID = q LRh LRm
preserve
clear
svmat double LRGRID, names(col)
tempfile LRGRID_dta
save "`LRGRID_dta'", replace
restore
* Load the LR grid results
use "`LRGRID_dta'", clear
* Plot the homoskedastic SupLR profile (like RATS)
twoway line LRh q, ///
ytitle("Likelihood ratio") ///
xtitle("Break value") ///
xline(`bestg', lpattern(dash) lcolor(gs8)) ///
yline(`bestLR', lpattern(dot) lcolor(gs10)) ///
title("Likelihood ratio vs break value") ///
note("Best threshold = `bestg' SupLR = `bestLR'") ///
legend(off)
di as txt "Best Threshold (hetero profile) gamma = " as res %9.4f `bestg'
di as txt "SupLR (hetero) = " as res %9.3f `bestLR'
/****************************************************
9) OBSERVED LR FUNCTIONALS — read LRGRID_dta safely
****************************************************/
preserve
use "`LRGRID_dta'", clear
gen double LR_obs = LRm
quietly summarize LR_obs, meanonly
local maxLR = r(max)
gen double z = exp(0.5*(LR_obs - `maxLR'))
quietly summarize z, meanonly
scalar AP_obs = ln(r(mean)) + 0.5*`maxLR'
quietly summarize LR_obs, meanonly
scalar AVG_obs = r(mean)
scalar SUP_obs = `maxLR'
restore
/*********************************************
10) PREP FOR BOOTSTRAP (gamma list + data)
*********************************************/
tempname EXCEED_SUP EXCEED_AVG EXCEED_AP
scalar `EXCEED_SUP' = 0
scalar `EXCEED_AVG' = 0
scalar `EXCEED_AP' = 0
tempfile GAMMA_LIST
preserve
clear
local NG : word count `GAMMAS'
set obs `NG'
gen double q = .
forvalues i = 1/`NG' {
local g : word `i' of `GAMMAS'
replace q = `g' in `i'
}
save "`GAMMA_LIST'", replace
restore
use "`data_dta'", clear
capture confirm variable S
if _rc {
__make_lags $YLIST, p($P)
__build_laglist, p($P)
__mark_sample, p($P)
gen byte S = S_lin & !missing(q)
}
replace S = S_lin & !missing(q) if missing(S)
/*********************************************
11) BOOTSTRAP (homoskedastic null: Sup/Avg/Exp)
— Gaussian wild bootstrap (RATS-aligned)
*********************************************/
forvalues b = 1/$NBOOT {
quietly {
* draw wild weights v_t on S==1
preserve
keep if S==1
keep S_idx
gen double v = rnormal()
tempfile WT
save "`WT'", replace
restore
* linear fits to get xb0 and e0 — drop per-variable before predicting
foreach y of global YLIST {
capture drop `y'_xb0
capture drop `y'_e0
quietly regress `y' $LAGLIST if S_lin
predict double `y'_xb0 if e(sample), xb
predict double `y'_e0 if e(sample), resid
}
* build bootstrap series y* = xb0 + v*e0 on S==1
preserve
keep if S==1
merge 1:1 S_idx using "`WT'", nogen
foreach y of global YLIST {
tempvar xb e
gen double `xb' = `y'_xb0
gen double `e' = `y'_e0
replace `y' = `xb' + v*`e'
drop `xb' `e'
}
* Sigma0* from stars
local rlist2
foreach y of global YLIST {
quietly regress `y' $LAGLIST
capture drop `y'_e0s
predict double `y'_e0s, resid
local rlist2 `rlist2' `y'_e0s
}
mkmat `rlist2', matrix(Us)
scalar Ts = rowsof(Us)
matrix S0s = (Us'*Us)/Ts
matrix symeigen Ls Vs = S0s
local ks = colsof(S0s)
scalar lnDetS0s = 0
forvalues i=1/`ks' {
if (Ls[`i',`i']<=0) continue
scalar lnDetS0s = lnDetS0s + ln(Ls[`i',`i'])
}
* LR(b) functionals over same grid — pass 1 (SUP)
local LRb_max = .
use "`GAMMA_LIST'", clear
quietly count
forvalues i = 1/`r(N)' {
local g = q[`i']
restore, preserve
quietly _tvar_lls, gamma(`g')
if !r(ok) continue
scalar LLhom = -0.5*( r(T) * r(lnDetSh) )
scalar LLlin = -0.5*( r(T) * lnDetS0s )
scalar LRb_ = 2*(LLhom - LLlin)
if missing(`LRb_max') | (LRb_ > `LRb_max') local LRb_max = LRb_
}
* pass 2 (AVG / EXP using LRb_max)
local sumLRb = 0
local sumAP = 0
local nGood = 0
use "`GAMMA_LIST'", clear
quietly count
forvalues i = 1/`r(N)' {
local g = q[`i']
restore, preserve
quietly _tvar_lls, gamma(`g')
if !r(ok) continue
scalar LLhom = -0.5*( r(T) * r(lnDetSh) )
scalar LLlin = -0.5*( r(T) * lnDetS0s )
scalar LRb2 = 2*(LLhom - LLlin)
local sumLRb = `sumLRb' + LRb2
local sumAP = `sumAP' + exp(0.5*(LRb2 - `LRb_max'))
local nGood = `nGood' + 1
}
if (`nGood'>0) {
scalar AVG_b = `sumLRb' / `nGood'
scalar AP_b = ln(`sumAP'/`nGood') + 0.5*`LRb_max'
scalar SUP_b = `LRb_max'
if (SUP_b > SUP_obs) scalar `EXCEED_SUP' = `EXCEED_SUP' + 1
if (AVG_b > AVG_obs) scalar `EXCEED_AVG' = `EXCEED_AVG' + 1
if (AP_b > AP_obs ) scalar `EXCEED_AP' = `EXCEED_AP' + 1
}
restore
}
if mod(`b',50)==0 di as txt "Bootstrap " `b' " / " $NBOOT
}
scalar p_sup = `EXCEED_SUP' / $NBOOT
scalar p_avg = `EXCEED_AVG' / $NBOOT
scalar p_exp = `EXCEED_AP' / $NBOOT
di as txt _n(1) "----------------------------------------------"
di as txt "Bootstrap (homoskedastic) LR functionals:"
di as txt "SupLR = " as res %9.3f SUP_obs " p = " %6.3f p_sup
di as txt "AvgLR = " as res %9.3f AVG_obs " p = " %6.3f p_avg
di as txt "ExpLR = " as res %9.3f AP_obs " p = " %6.3f p_exp
di as txt "----------------------------------------------"
log close _all
exit
**# End of ProgramConclusion:
As we have seen in this blog, it is possible to translate RATS code for the threshold VAR into Stata Code in a few hours relying on iterations with ChatGPT 5. The files for replicating the results in this blog will be available on my GitHub.
Further reading
Balke, N. S. (2000). Credit and economic activity: credit regimes and nonlinear propagation of shocks. Review of Economics and Statistics, 82(2), 344-349.