If you are a macroeconomist interested in impulse response function analysis, you need to watch this presentation by Christian Wolf during the 40th Annual NBER Conference on Macroeconomics, the paper is available here:
Key Takeaways
- Small mistakes in lag selection are relatively harmless in local projections but potentially very costly in VARs.
- This is why using information criteria (e.g. AIC) to guide lag selection for an auxiliary VAR, and then applying that lag length to LPs, is a reasonable strategy.
- The equivalence between VARs and LPs only holds when VARs are estimated with a sufficiently large number of lags and large samples.
- With long lags, VARs can match the robustness of LPs and yield reliable inference; with too few lags, they risk smooth but biased results.
- In practice, LPs offer robustness by construction, while VARs only achieve the same reliability when carefully specified with enough dynamics.
- A misspecified VAR can give biased results that look deceptively precise.
- Local projections are noisier in finite samples, yet robust to misspecification and flexible in design.
- The divergence between VAR and LP IRFs reflects methodology, not necessarily error.
I covered their previous paper in a previous blog that you can access here:
I sincerely appreciate the effort that has been made to make recommendations to macroeconomists.
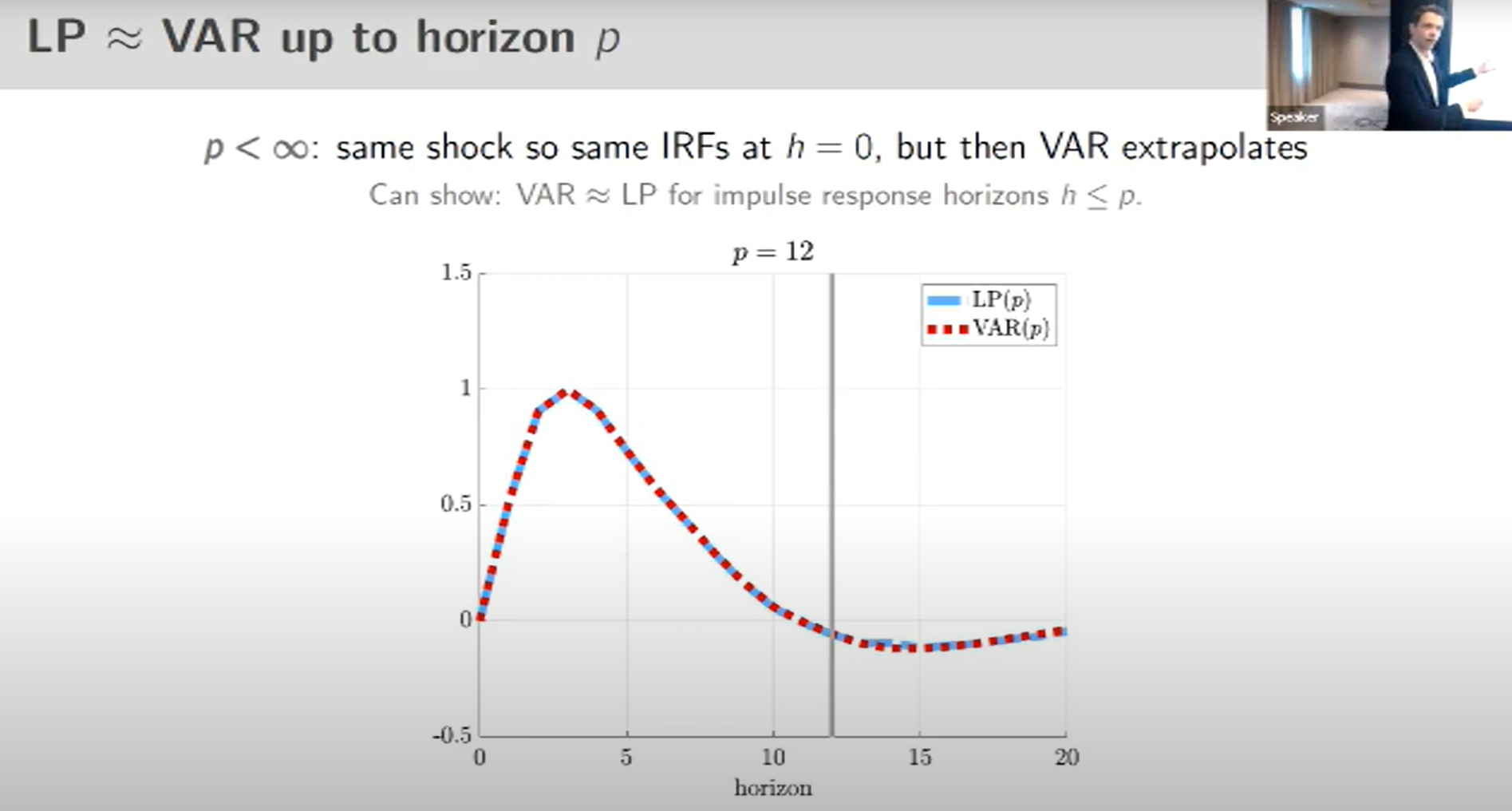
With infinite lags VAR and LP impulse response functions are the same:
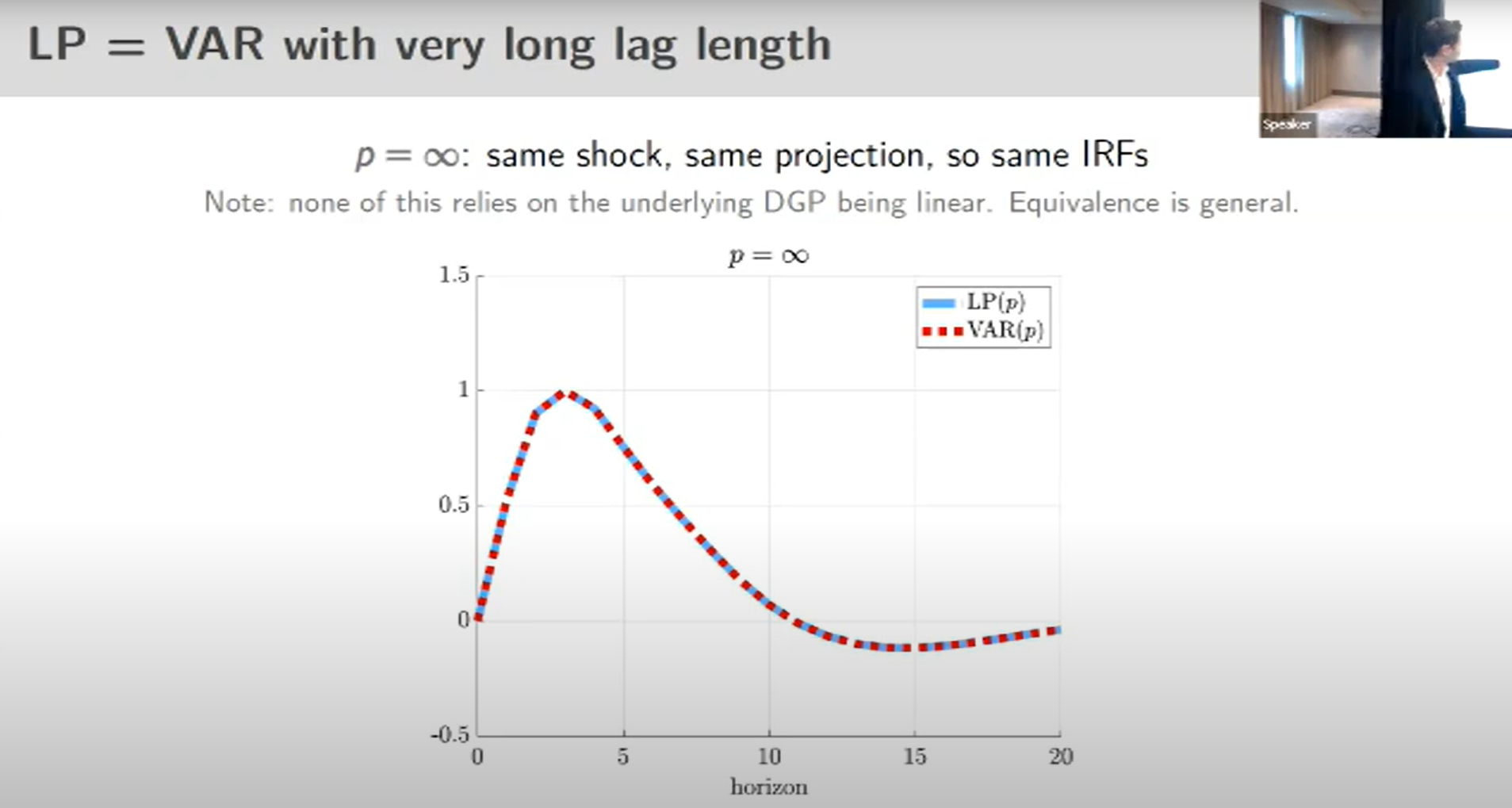
If the horizon is higher than the number of lags included in the VAR, then VAR and LP impulse response functions are the same until the horizon p.
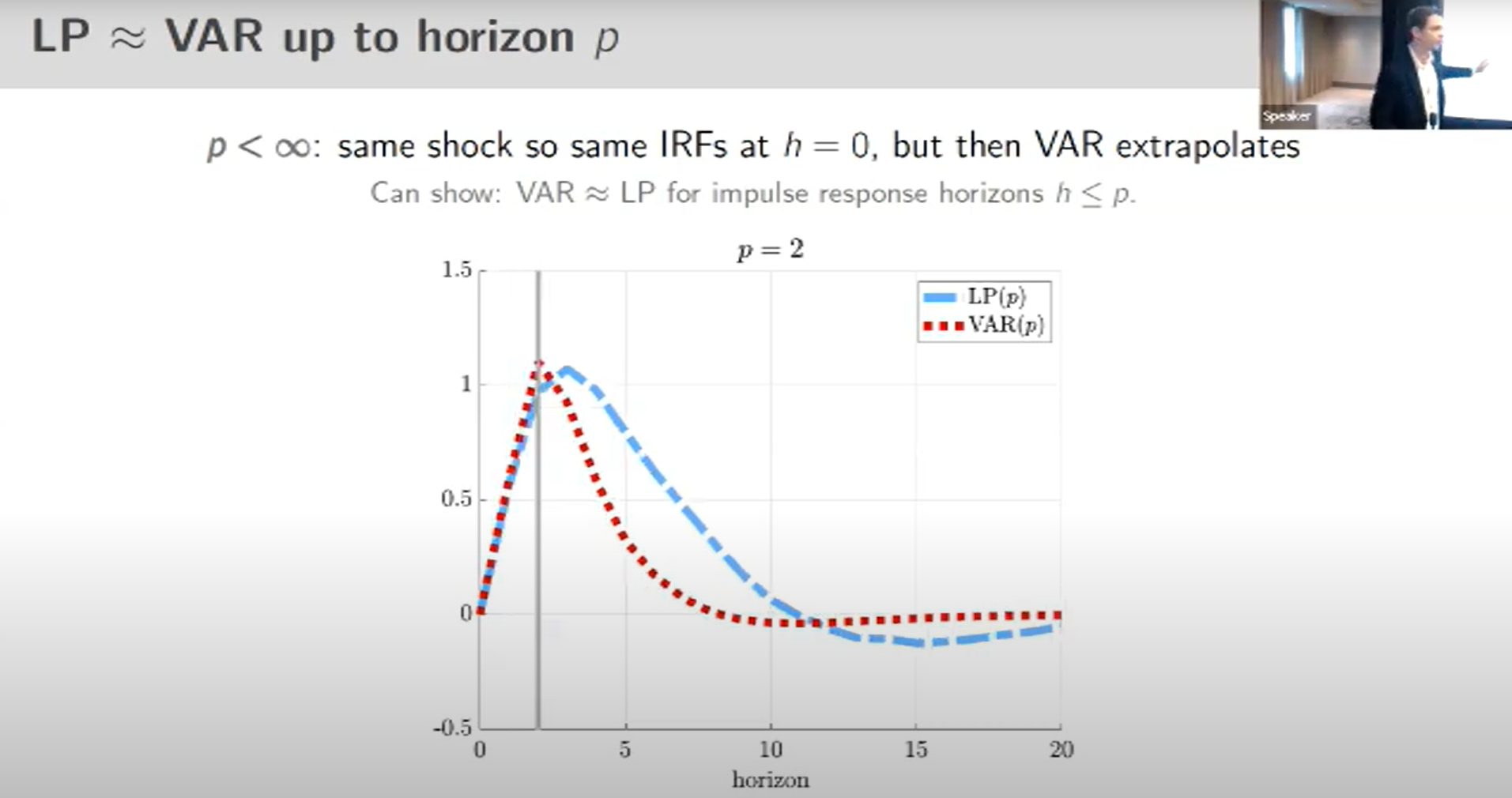
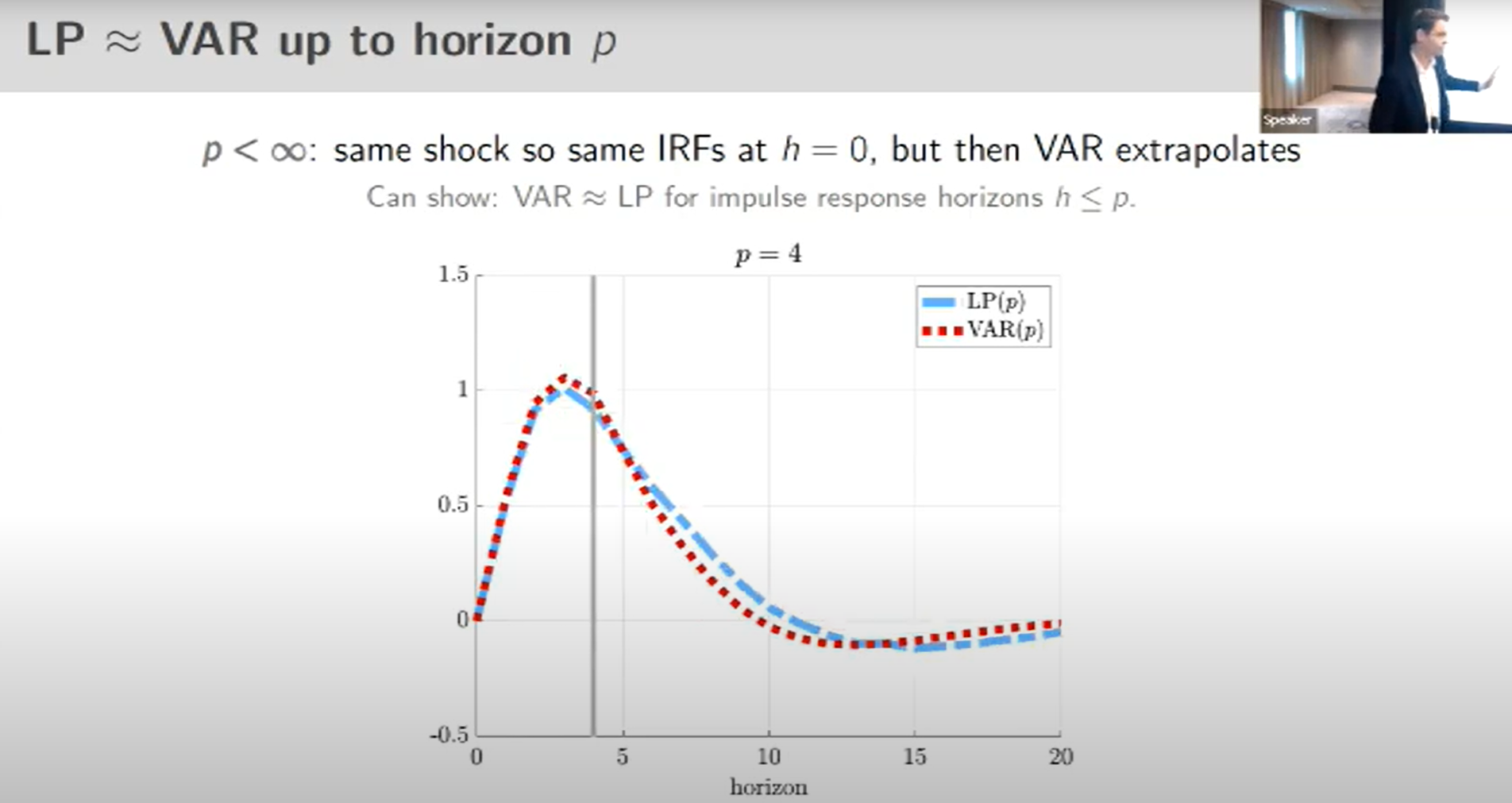
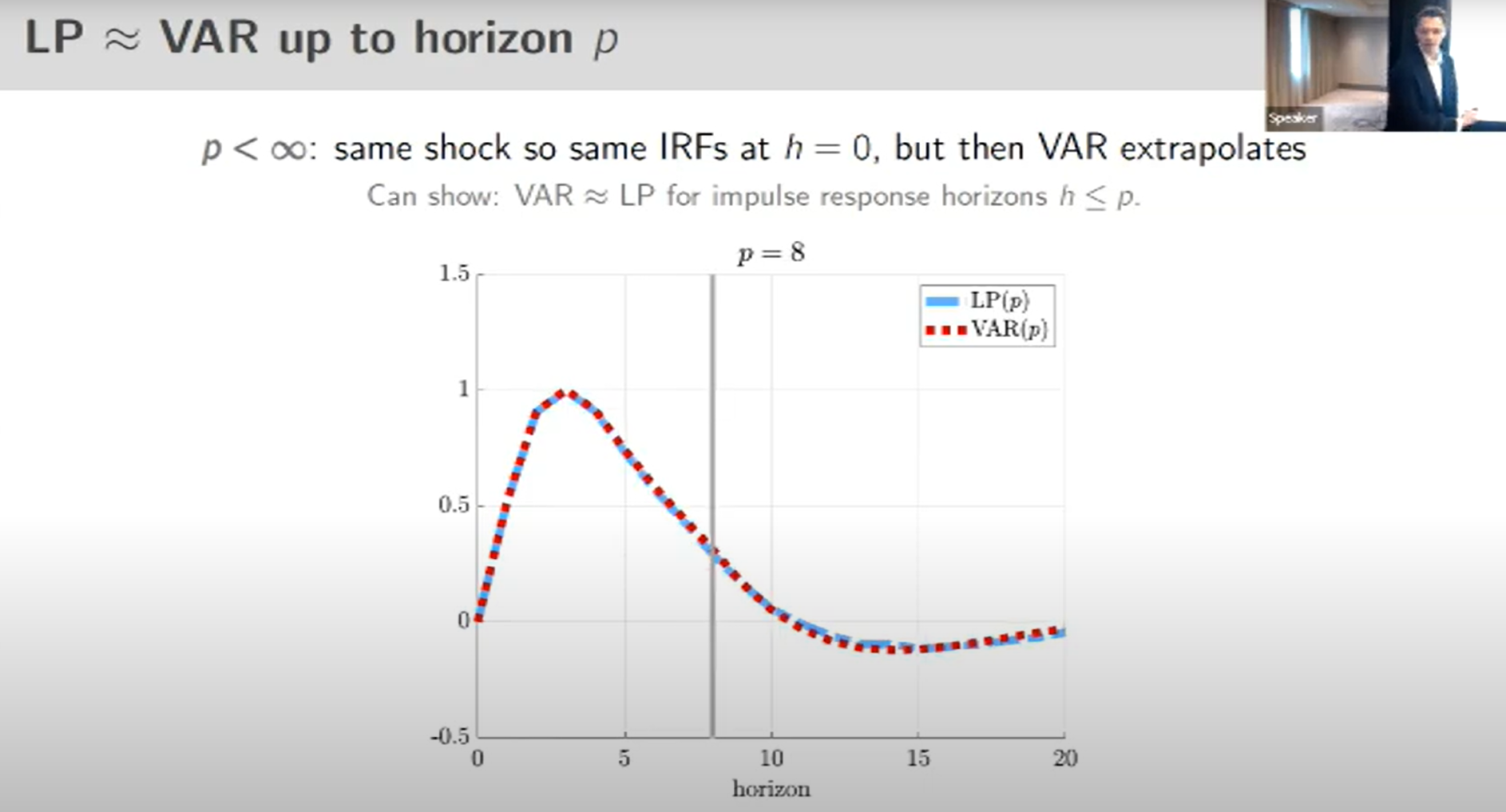
Their conclusion on the best practice:

From the discussion of the paper:
“Mikkel Plagborg-Møller followed up to reinforce the central empirical finding of the paper: Small mistakes in lag selection are relatively harmless in LPs but potentially very costly in VARs. Using AIC to select the number of lags in an auxiliary VAR and applying that to LPs is therefore appropriate, since LPs are more robust to modest misspecification.”
“The authors agreed with this interpretation and emphasized that their equivalence result hinges on using a sufficiently large number of lags. Only in this case do VARs achieve the same robustness to misspecification and reliable inference properties as LPs. The authors mentioned that this long-lag equivalence is already discussed in their paper. They emphasized that the performance gap disappears, and VARs achieve the same robustness as LPs, precisely when VARs have enough lags, and only then.”
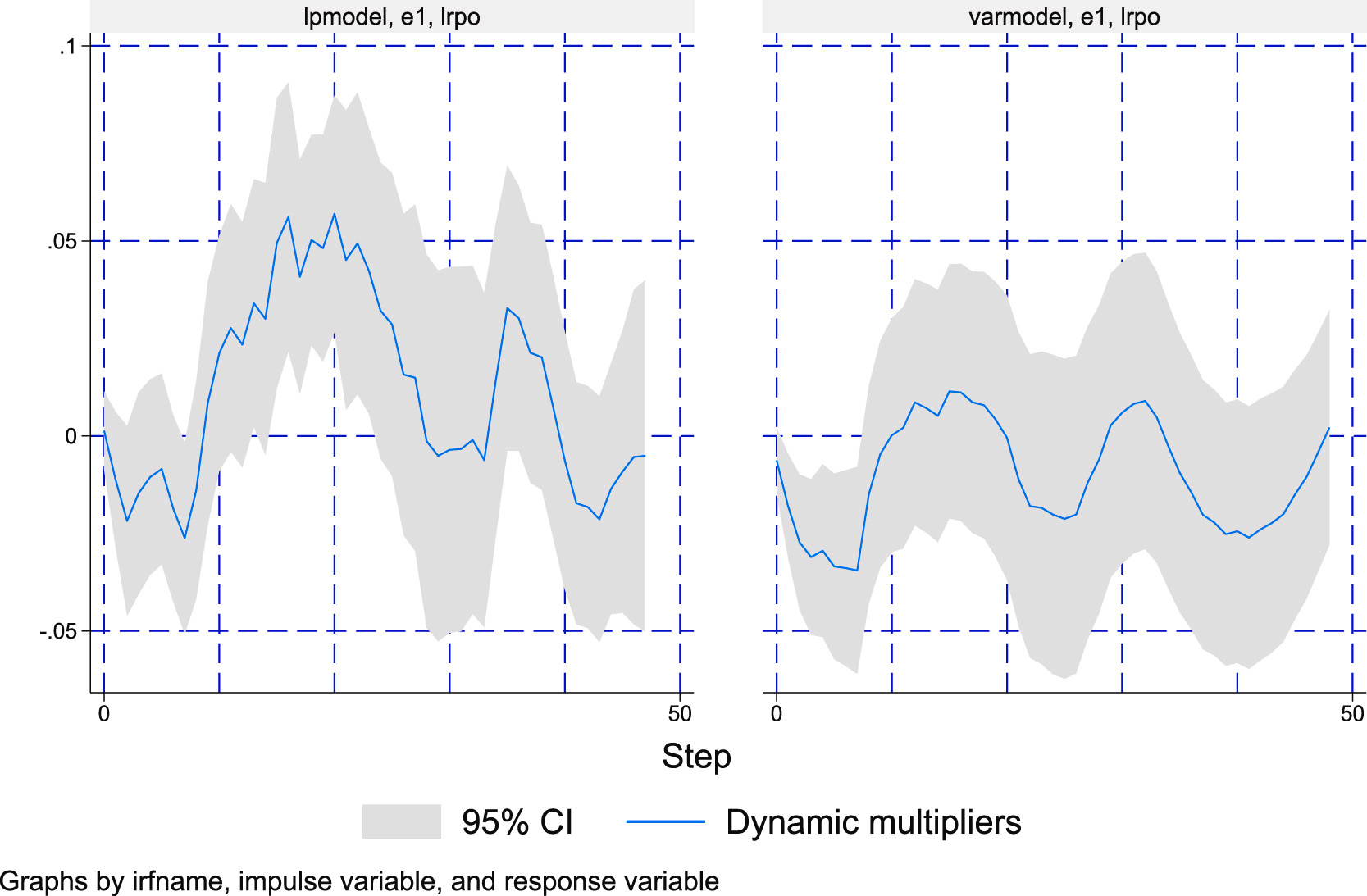
A concrete illustration comes from our recent study in Energy Economics (Mignon & Saadaoui, 2024) on the impact of political tensions and geopolitical risks on oil prices. In that paper, we estimated both VAR- and LP-based impulse responses and compared their behavior. The VARs, specified with 24 lags to clean the residuals, delivered smooth and stable IRFs, which is consistent with a correctly specified and stable dynamic system. The LPs, by contrast, produced noisier and more volatile responses, particularly at longer horizons, even though both approaches should be asymptotically equivalent in expectation below horizon 24. This divergence reflects finite-sample realities rather than misspecification: with limited observations, LPs accumulate estimation noise horizon by horizon, while VARs impose structure that smooths dynamics but are more sensitive to model assumptions. In practice, the two approaches are complementary—the VAR gains efficiency under correct specification, while the LP provides a robustness check against possible misspecification. Crucially, both methods in our application pointed to the same substantive conclusion—geopolitical shocks push oil prices upward—underscoring that the results are robust despite the finite-sample differences in shape and precision.
Conclusion
The contrast between local projections and VARs highlights a fundamental trade-off in applied macroeconometrics. VARs provide smooth and precise impulse responses when they are correctly specified, but if they omit relevant dynamics or impose incorrect restrictions, their efficiency comes at the cost of bias. Local projections, by estimating each horizon directly, avoid this pitfall and remain robust to misspecification, though at the expense of higher finite-sample variability and noisier estimates. As our application in Energy Economics (Mignon & Saadaoui, 2024) shows, both methods converged on the same conclusion—geopolitical shocks raise oil prices—even if the VAR appeared smoother and the LP more erratic. The key lesson is that VARs are only as trustworthy as their specification, while the noise of LPs offers a safeguard against spurious smoothness. Used together, the two approaches provide a more reliable picture of the true underlying dynamics.
References
Mignon, Valérie & Saadaoui, Jamel, 2024. “How do political tensions and geopolitical risks impact oil prices?,” Energy Economics, Elsevier, vol. 129(C), https://www.sciencedirect.com/science/article/pii/S014098832300717X
José Luis Montiel Olea & Mikkel Plagborg-Møller & Eric Qian & Christian K. Wolf, 2024. “Double Robustness of Local Projections and Some Unpleasant VARithmetic,” NBER Working Papers 32495, National Bureau of Economic Research, Inc., https://www.nber.org/papers/w32495
José Luis Montiel Olea & Mikkel Plagborg-Møller & Eric Qian & Christian K. Wolf, 2025. “Local Projections or VARs? A Primer for Macroeconomists,” NBER Chapters, in: NBER Macroeconomics Annual 2025, volume 40, National Bureau of Economic Research, Inc, https://www.nber.org/papers/w33871