In my previous blog, I recall that we can demonstrate in a few steps that the sample variance is an unbiased estimator of the population variance when we divide by n-1:
\begin{aligned}
E(S^2)&=\Big[\frac{\Sigma_{i=1}^n (X_i-\bar X)^2}{n-1}\Big]\\
&=\sigma^2
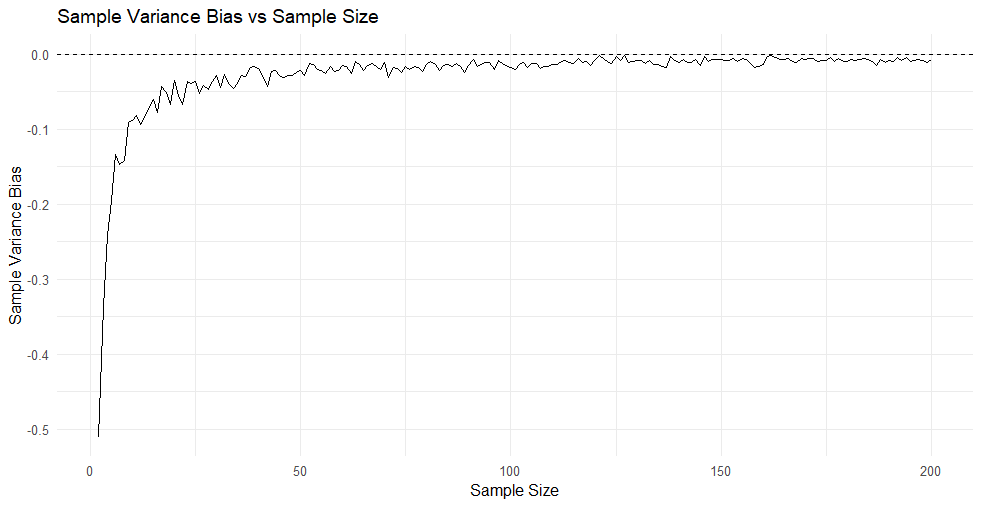
\end{aligned}In this other blog, I used the new Wolfram function AIAssistant to illustrate the sample variance bias in R and in Mathematica. We can also visualize that the variance sample biais decrease with the sample size. The R code is presented below:
# Load required libraries
library(ggplot2)
# Set the parameters
pop_mean <- 0
pop_sd <- 1
pop_size <- 10000
sample_sizes <- seq(2, 200, 1)
num_samples <- 1000
# Create the population
set.seed(123)
population <- rnorm(pop_size, mean = pop_mean, sd = pop_sd)
# Function to compute sample variance bias
compute_sample_variance_bias <- function(sample_size) {
sample_vars <- replicate(num_samples, {
sample <- sample(population, size = sample_size)
var(sample) * (sample_size - 1) / sample_size
})
mean(sample_vars) - pop_sd^2
}
# Calculate sample variance bias for each sample size
sample_variance_biases <- sapply(sample_sizes, compute_sample_variance_bias,
USE.NAMES = FALSE)
# Create a data frame for plotting
data <- data.frame(SampleSize = sample_sizes, Bias = sample_variance_biases)
# Generate the graph
ggplot(data, aes(x = SampleSize, y = Bias)) +
geom_line() +
geom_hline(yintercept = 0, linetype = "dashed") +
theme_minimal() +
labs(x = "Sample Size", y = "Sample Variance Bias",
title = "Sample Variance Bias vs Sample Size")
This give the following representation:
If you are not familiar with the R language, you can use the new Wolfram function AIAssistant to explain each step in the code:
This R code generates a plot to show how sample size affects the bias of a sample variance estimator. Here is what each step does:
1. The ggplot2 library is loaded.
2. The population mean, standard deviation, size, and sample sizes are defined. pop_mean is the mean of the population; pop_sd is its standard deviation; pop_size is the size of the population; sample_sizes is a sequence of sample sizes ranging from 2 to 200.
3. The population is generated using the rnorm() function with a mean of pop_mean and a standard deviation of pop_sd. The set.seed() function is used to ensure that the same random numbers are generated each time the code is run.
4. A function compute_sample_variance _bias() is defined to compute the bias of a sample variance estimator for a given sample size. This function takes a sample size as input and returns the bias of the sample variance estimator. It does this by first replicating the sampling process num_samples times for a given sample size, then computing the sample variance for each replicate, adjusting for the bias in the sample variance estimator, and finally computing the mean of the adjusted sample variances.
5. sapply() is used to apply the compute_sample_variance _bias() function to each element of sample_sizes and return the sample variance bias for each sample size in a vector called sample_variance_biases.
6. A data frame called data is created with two columns: SampleSize, which contains the sample sizes, and Bias, which contains the corresponding sample variance biases.
7. A graph is generated using ggplot(). The data frame data is specified as the data source for the plot, and aes() is used to map the SampleSize column to the x-axis and the Bias column to the y-axis. geom_line() is used to plot a line connecting each point, and geom_hline() is used to add a dashed horizontal line at y = 0. theme_minimal() is used to set a simple theme, and labs() is used to add labels for the x-axis, y-axis, and title of the plot.I wanted to have a detailed explanation on the loop:
Explained me in a detailed way the following part
# Function to compute sample variance bias
compute_sample_variance_bias <- function(sample_size) {
sample_vars <- replicate(num_samples, {
sample <- sample(population, size = sample_size)
var(sample) * (sample_size - 1) / sample_size
})
mean(sample_vars) - pop_sd^2
}The result:
This part of the code defines a function called compute_sample_variance _bias() that computes the bias of a sample variance estimator for a given sample size.
Here is how the function works:
1. The function takes a single input called sample_size, which represents the size of the sample.
2. Inside the function, the replicate() function is used to generate num_samples replicates of a random sample of size sample_size from the population. For each replicate, the sample() function is used to randomly sample sample_size observations from the population.
3. The variance of each replicate is computed using the var() function, which calculates the sample variance (i.e., the sample standard deviation squared) of the random sample. However, the sample variance estimator is biased, so an adjustment is made by multiplying by (sample_size-1)/sample_size.
4. The adjusted sample variances are stored in a vector called sample_vars.
5. The mean of the sample_vars vector is calculated using the mean() function.
6. The population variance pop_sd^2 is subtracted from the mean of sample_vars. This difference represents the bias in the sample variance estimator for a given sample size.
7. The bias is returned as the output of the function.
In summary, this function takes a sample size as input, generates multiple random samples of that size from a population, computes the sample variances for each sample, adjusts for bias in the sample variance estimator, calculates the mean of the adjusted sample variances, and subtracts the population variance to return the bias in the sample variance estimator.I asked the AI research assistant to write the equivalent in Mathematica :
(*Load required package*)Needs["GeneralUtilities`"];
(*Set the parameters*)
popMean = 0;
popSD = 1;
popSize = 10000;
sampleSizes = Range[2, 200, 1];
numSamples = 1000;
(*Create the population*)
SeedRandom[123];
population =
RandomVariate[NormalDistribution[popMean, popSD], popSize];
(*Function to compute sample variance bias*)
computeSampleVarianceBias[sampleSize_] :=
Module[{sampleVars},
sampleVars =
Table[Block[{sample}, sample = RandomSample[population, sampleSize];
Variance[sample]*(sampleSize - 1)/sampleSize], numSamples];
Mean[sampleVars] - popSD^2]
(*Calculate sample variance bias for each sample size*)
sampleVarianceBiases = computeSampleVarianceBias /@ sampleSizes;
(*Create a data frame for plotting*)
data = Transpose[{sampleSizes, sampleVarianceBiases}];
(*Generate the graph*)
ListLinePlot[data, Frame -> True,
FrameLabel -> {"Sample Size", "Sample Variance Bias"},
PlotLabel -> "Sample Variance Bias vs Sample Size",
Epilog -> {Dashed, Line[{{2, 0}, {200, 0}}]},
BaseStyle -> {FontFamily -> "Source Sans Pro", FontSize -> 12}]
We can see that the downward bias almost disappears from 30 observations.
Please note that the files for replicating this blog are (or will be) available here: https://github.com/JamelSaadaoui/EconMacroBlog

Leave a Reply