In a previous blog, I showed how to draw local projection’s impulse response function with Driscoll-Kraay inference in Stata. This is the picture what you get:
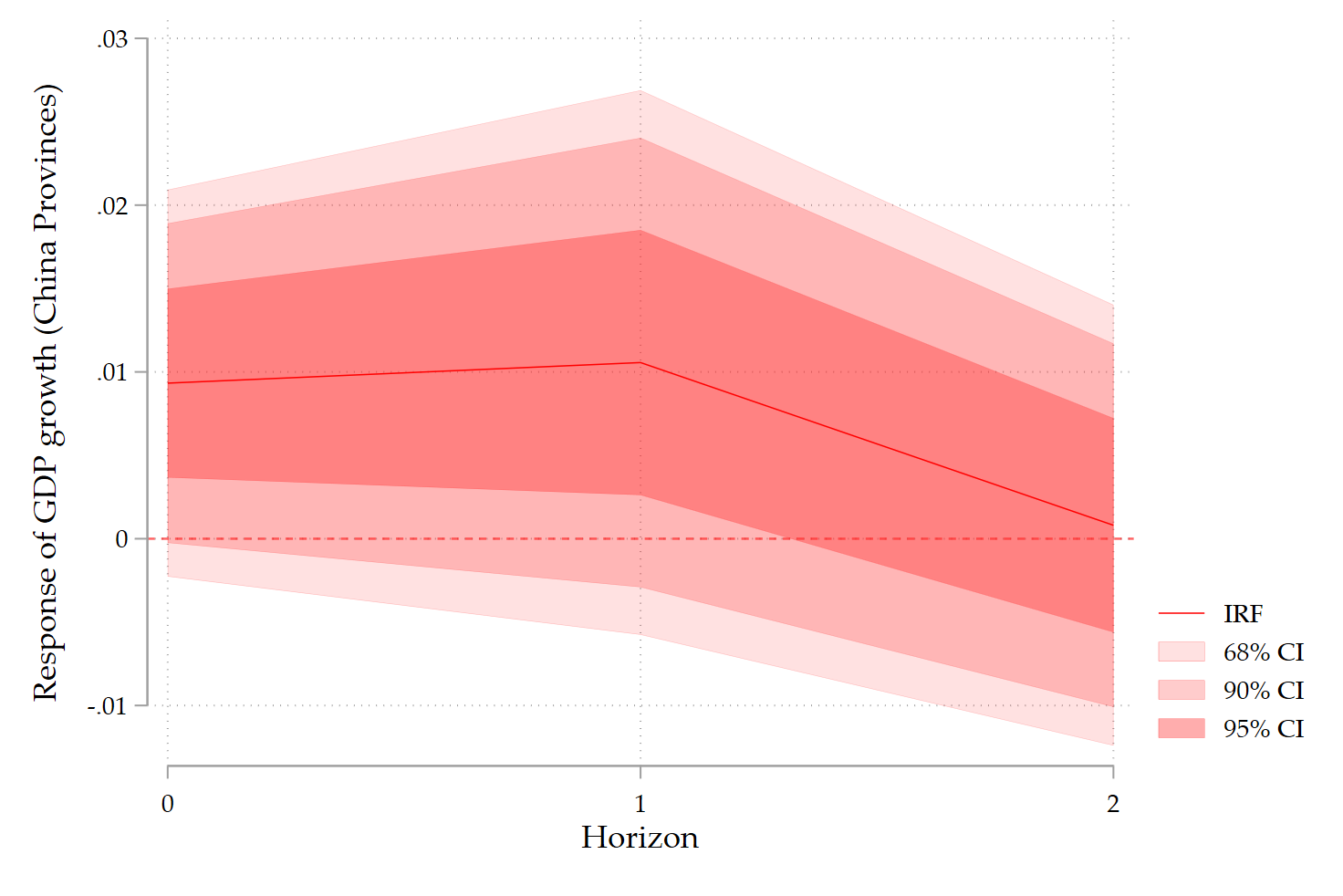
But, Alfonso Ugarte on LinkedIn told me that you can also use locproj to get a similar picture (while not yet documented in the locproj help):
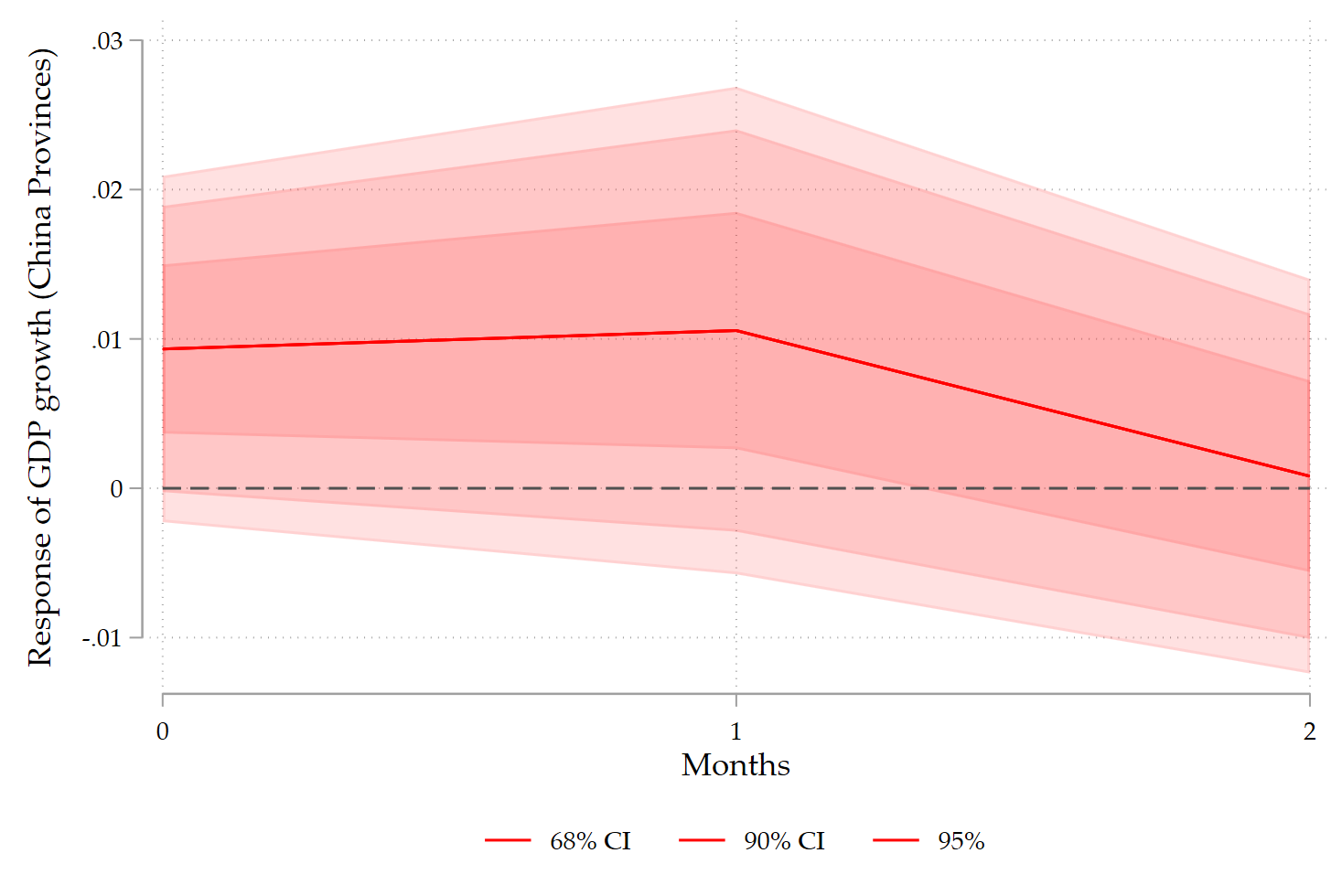
Full code below for pedagogical purposes:
foreach h in 68 90 95 {
locproj D.GDP, shock(z_D_LUSA) ///
h(2) yl(2) sl(0) zero ///
c(L(1/2).(CPI TRADE GFCF POP TOT)) fe ///
conf(`h') lcolor(sand) ///
ttitle("Horizon") title(`"US-China"') ///
noisily stats save irfname(iUS`h') grname(US`h') met(xtscc)
}
lpgraph iUS68 iUS90 iUS95, h(2) tti(Months) ///
nolegend ///
tti(Months) ti1(DK-LP) ///
title("") ///
lab1(68% CI) lab2(90% CI) lab3(95%) ///
lc1(red) lc2(red) lc3(red) ///
z grname(DK) grsave(DK) as(png) ///
xtitle("Horizon") ///
ytitle("Response of GDP growth (China Provinces)")