Using the moment generating functions to find moments: a simple example

The moment generating function can be quite obscure for students. We have a definition here. Quite obscure, isn’t it! In this blog, I will show a simple example that will convince you that moment generating functions are very practical… to generate moments.

The example is based on the very pedagogical YouTube video of Lawrence Leemis.

In the example, you have to use the moment generating function to find E[X], E[X²], and E[X³] for the continuous random variable X with the following probability density function:

f(x)=e^{-x} \quad x>0

The moment generating function of X is by definition over the support x > 0:

M(t)  =E\left[e^{t X}\right]

By the definition of the expected value of a random variable with density, we have:

=\int_0^{\infty} e^{t x} e^{-x} d x

From the exponent laws, we have:

=\int_0^{\infty} e^{(t-1) x} d x

For example, see e^{-3 x} versus e^{+3 x} on Wolfram Alpha with the following prompt command Plot[{E^(-3 x), E^(3 x)}, {x, -1., 1.}]:

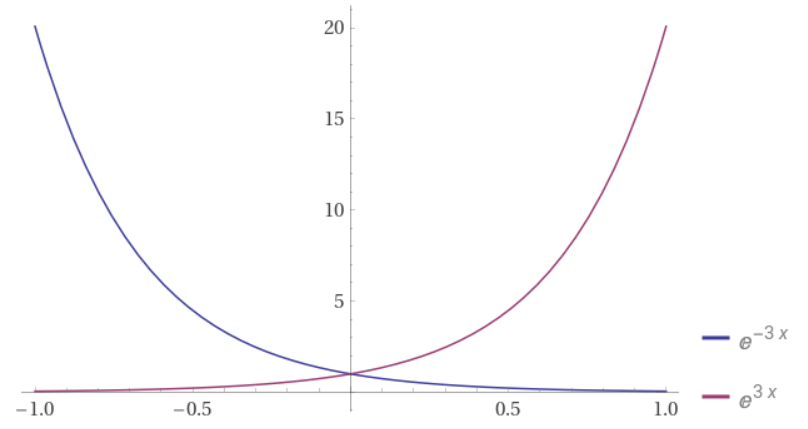
We can see from above that (t-1) needs to be inferior to 1 in order to have a convergent integral in blue. So let’s put that (t-1) < 0.

For the integrand e^{(t-1) x}, substitute u =(t-1) x and d u = (t-1) d x. Check this with Wolfram Alpha :

=\frac{1}{t-1} \int e^u d u

Come back to the integral over the support x > 0:

\frac{1}{t-1}\left[e^{(t-1) x}\right]_0^{\infty}

You can easily see on Wolfram Alpha with the following prompt Integrate[E^((-1 + t) x), {x, 0, Infinity}] that the moment generating function is

M(t)=\frac{1}{1-t} \quad t-1<0

The moment generation function is defined for values of t inferior to 1. Indeed, for the value of t = 0, it exists some values that satisfy -h < t < h. For example, h could be equal to 1/3 or 1/2 or some other values. That suffices to have a valid moment generating function.

I can now generate the three first moments quite easily by taking the first three derivatives of the moment generating function:

\small{M^{\prime}(t)=(1-t)^{-2} \quad M^{\prime \prime}(t)=2(1-t)^{-3} \quad M^{\prime \prime \prime}(t)=6(1-t)^{-4}}

for t < 1. Using t = 0 ( for the value of t = 0, it exists some values that satisfy -h < t < h) as an argument yields

\small{E[X]=1 \quad E\left[X^2\right]=2 \quad E\left[X^3\right]=6}

This is easier than

E\left[X^3\right]=\int_0^{\infty} x^3 e^{-x} d x

where you have to use integration by parts.